0 49549 49557 49563 49567 49573 49575 49579 49585 49587 49593 49599 49603 49605 49609 49615 49617 49623 49627 49629 49633 49635 49639 49641 49643 49644 49645 49647 49648 49649 49651 49653 49657 49659 49663 49665 49669 49675 49677 49683 49687 49689 49693 49699 49705 49707 49713 49717 49719 49725 49729 49735 49743 447348
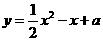 与x轴交于A,B两点,与y轴交于点C,其顶点在直线y=-2x上.
与x轴交于A,B两点,与y轴交于点C,其顶点在直线y=-2x上.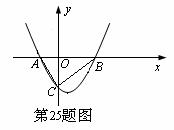
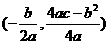 ,∴x=1,∵顶点在直线y=-2x上,所以y=-2,即顶点坐标为(1,-2),∴-2=
,∴x=1,∵顶点在直线y=-2x上,所以y=-2,即顶点坐标为(1,-2),∴-2=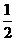 -1+a,即a=-
-1+a,即a=-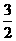 4;(2)二次函数的关系式为
4;(2)二次函数的关系式为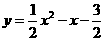 ,当y=0时,
,当y=0时,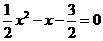 ,解之得:
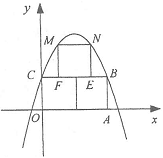
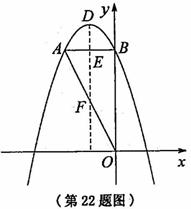
,解之得: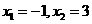 ,即A(-1,0),B(3,0);(3)如图所示:直线BD//AC,AD//BC,因为A(-1.0),C(0,
,即A(-1,0),B(3,0);(3)如图所示:直线BD//AC,AD//BC,因为A(-1.0),C(0,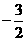 ),所以直线AB的解析式为
),所以直线AB的解析式为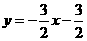 ,所以设BD的解析式为
,所以设BD的解析式为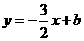 ,因为B(3,0),所以b=
,因为B(3,0),所以b=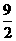 ,直线BD的解析式为:
,直线BD的解析式为: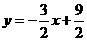 ,同理可得:直线AD的解析式为:
,同理可得:直线AD的解析式为: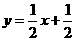 ,因此直线BD与CD的交点坐标为:(2,
,因此直线BD与CD的交点坐标为:(2,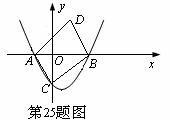
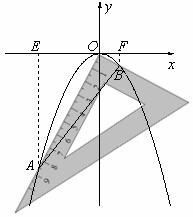
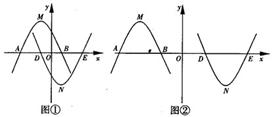
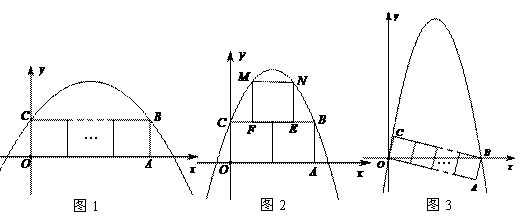
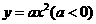 的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点O,两直角边与该抛物线交于A、B两点,请解答以下问题:
的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点O,两直角边与该抛物线交于A、B两点,请解答以下问题: (如图1),求
(如图1),求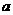 的值;
的值;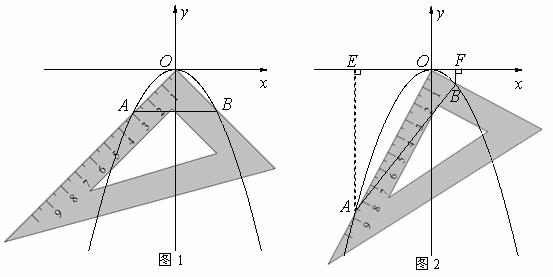
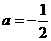 .
. 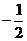 ),
),
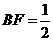 . 又∵∠AOB=90°,易知∠AOE=∠OBF,又∠AEO=∠OFB=90°,
. 又∵∠AOB=90°,易知∠AOE=∠OBF,又∠AEO=∠OFB=90°,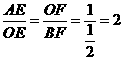 ∴AE=2OE,
∴AE=2OE, 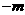 ,
,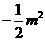 )(m>0),则OE=m,
)(m>0),则OE=m,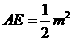 ,∴
,∴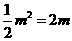
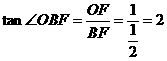
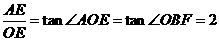 ,∴AE=2OE,
,∴AE=2OE,
 ,
,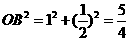 ,
,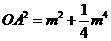 ,
,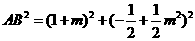 ,
, 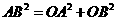 ,
,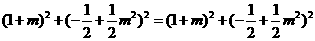 ,
,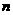 ,
,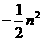 )(n>0),
)(n>0),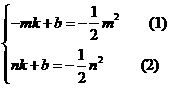 ,
,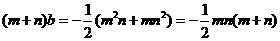 ,
,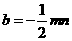
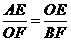 ,∴
,∴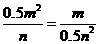 ,∴mn=4,
,∴mn=4,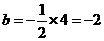 .由此可知不论k为何值,直线AB恒过点(0,-2),
.由此可知不论k为何值,直线AB恒过点(0,-2),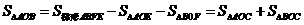 ,可得
,可得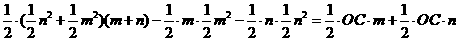 ,
,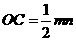 .
. 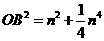 ,
,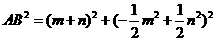 ,
,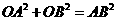 ,得:
,得: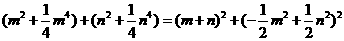 ,
,

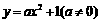 ,
,  抛物线经过
抛物线经过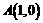 ,
,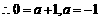 ,
,
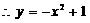 .
. 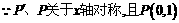 ,
,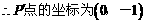
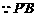 ∥
∥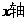 ,
,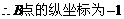 ,
,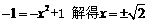 ,
,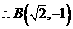 ,
,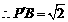 .
.
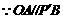 ,
, ∽
∽ ,
,  .
. 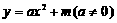
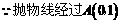 ,
,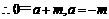
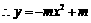 .
. 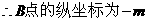 ,
, 
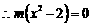 ,
,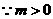 ,
,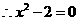 ,
,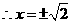 ,
,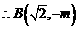 ,
,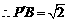 ,
,
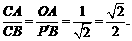
 .
. 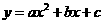 经过点A、B和D(4,
经过点A、B和D(4,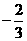 )。
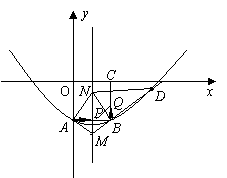
)。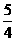 时,在抛物线上是否存在点R,使得以点P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由。
时,在抛物线上是否存在点R,使得以点P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由。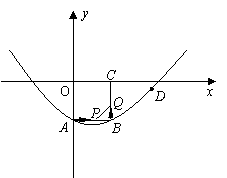

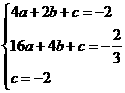 解得
解得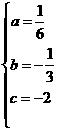
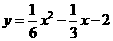
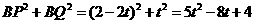 (0≤t≤1)
(0≤t≤1)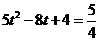 解得t=
解得t=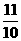 (不合题意,舍去)
(不合题意,舍去)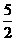 )或(1,
)或(1,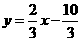
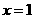 时,
时,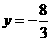 ,故点M的坐标为(1,
,故点M的坐标为(1,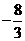 )
)
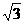 x2+
x2+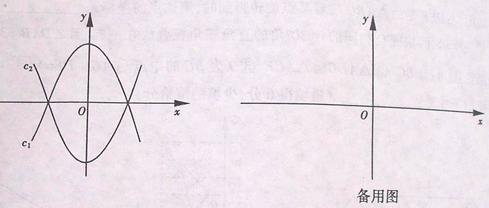
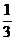 AE时,如图①,(-1+m)-(-1-m)=
AE时,如图①,(-1+m)-(-1-m)=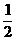

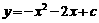 经过点A.
经过点A.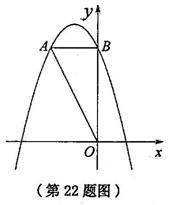
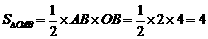
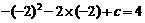 ,∴c=4
,∴c=4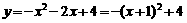 ,
,
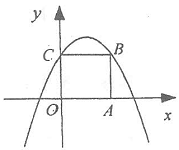
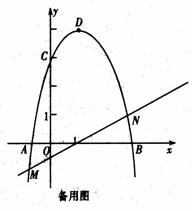
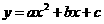 (a≠0)与x轴交与点A(-1,0)、B(3,0)两点,抛物线交y轴于点C(0,3),点D为抛物线的顶点.直线y=x-1交抛物线于点M、N两点,过线段MN上一点P作y轴的平行线交抛物线于点Q.
(a≠0)与x轴交与点A(-1,0)、B(3,0)两点,抛物线交y轴于点C(0,3),点D为抛物线的顶点.直线y=x-1交抛物线于点M、N两点,过线段MN上一点P作y轴的平行线交抛物线于点Q.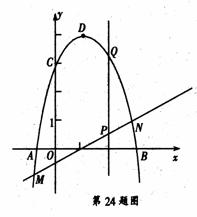
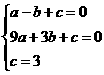 解得:
解得: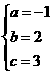
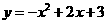 =
=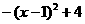 ,顶点坐标为(1,4).
,顶点坐标为(1,4).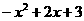 ),
),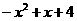 =
= 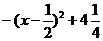
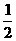 时,线段PQ最长为
时,线段PQ最长为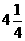 。
。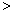 0)与双曲线y=
0)与双曲线y=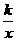 相交于点A,B. 已知点B的坐标为(-2,-2),点A在第一象限内,且tan∠AOx=4. 过点A作直线AC∥x轴,交抛物线于另一点C.
相交于点A,B. 已知点B的坐标为(-2,-2),点A在第一象限内,且tan∠AOx=4. 过点A作直线AC∥x轴,交抛物线于另一点C.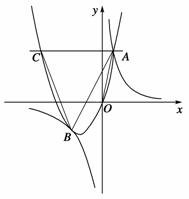
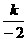 ,∴k=4.
,∴k=4.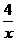 .
. 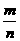 =4, 即m=4n.…②
=4, 即m=4n.…②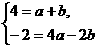 解得a=1,b=3;
解得a=1,b=3;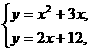 得
得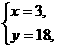 所以点D的坐标是(3,18)
所以点D的坐标是(3,18)