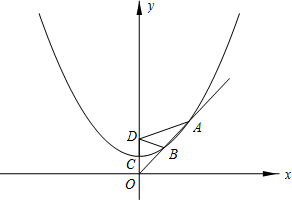
摘要： 已知抛物线的顶点是C.并经过点为一定点． ⑴求含有常数a的抛物线的解析式, ⑵设点P是抛物线上任意一点.过P作PH⊥x轴.垂足是H.求证:PD=PH, ⑶设过原点O的直线与抛物线在第一象限相交于A.B两点.若DA=2DB.且,求a的值． [答案]解:⑴设抛物线的解析式为 ∵点D在抛物线上. ∴ ∴抛物线的解析式为 ⑵设抛物线上一点P(x,y).过P作PH⊥x轴.PG⊥y轴.在中.由勾股定理得: ∵ ∴ ∴ ∴PD=PH. ⑶过B点BE⊥x轴.AF⊥y轴. 由⑵的结论:BE=DB AF=DA ∵DA=2DB ∴AF=2BE ∴AO=2BO ∴B是OA的中点 ∵C是OD的中点 连接BC ∴ 过B作BR⊥y轴. ∵BR⊥CD ∴CR=DR, . ∴B点的纵坐标是.又点B在抛物线上 ∴ ∴ ∵ ∴ ∴B(.) AO=2OB, ∴ 所以. ∴. ∵ ∴

网址：http://m.1010jiajiao.com/timu3_id_496472[举报]