摘要:10.如图.已知⊙O的半径为2.弦BC的长为.点A为弦BC所对优弧上任意一点. ⑴求∠BAC的度数, ⑵求△ABC面积的最大值. (参考数据:sin60°=.cos30°=.tan30°=.) [答案](1)过点O作OD⊥BC于点D, 连接OA. 因为BC=.所以CD==. 又OC=2.所以=.即=. 所以∠DOC=60°. 又OD⊥BC.所以∠BAC=∠DOC=60°. (2)因为△ABC中的边BC的长不变.所以底边上的高最大时.△ABC面积的最大值,即点A是的中点时.△ABC面积的最大值. 因为∠BAC=60°.所以△ABC是等边三角形. 在Rt△ADC中.AC=.DC=, 所以AD===3. 所以△ABC面积的最大值为×3×=3.
网址:http://m.1010jiajiao.com/timu3_id_496140[举报]
 如图,已知⊙O的半径为13,弦AB=10,CD=24,则图中阴影部分的面积是( )
如图,已知⊙O的半径为13,弦AB=10,CD=24,则图中阴影部分的面积是( )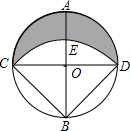 如图,已知⊙O的半径为R,直径AB⊥CD以B为圆心,以BC为半径作弧CED.求弧CED与弧CAD围成的新月形ACED的面积S.
如图,已知⊙O的半径为R,直径AB⊥CD以B为圆心,以BC为半径作弧CED.求弧CED与弧CAD围成的新月形ACED的面积S.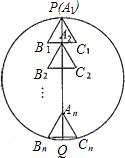
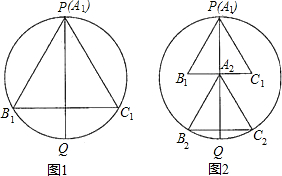
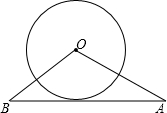 如图,已知⊙O的半径为1,OA=2,OB=
如图,已知⊙O的半径为1,OA=2,OB=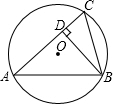 如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则tan∠CBD的值等于( )
如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则tan∠CBD的值等于( )