摘要： 如图.射线PG平分∠EPF.O为射线PG上一点.以O为圆心.10为半径作⊙O.分别与∠EPF两边相交于A.B和C.D.连结OA.此时有OA∥PE. (1)求证:AP＝AO, (2)若弦AB＝12.求tan∠OPB的值, (3)若以图中已标明的点(即P.A.B.C.D.O)构造四边形.则能构成菱形的四个点为 .能构成等腰梯形的四个点为 或 或 . 证明:(1)∵PG平分∠EPF. ∴∠DPO=∠BPO . ∵OA//PE. ∴∠DPO=∠POA . ∴∠BPO=∠POA. ∴PA=OA, --2分 解:(2)过点O作OH⊥AB于点H.则AH=HB=AB.--1分 ∵ tan∠OPB=.∴PH=2OH. --1分 设OH=.则PH=2. 由(1)可知PA=OA= 10 .∴AH=PH-PA=2-10. ∵. ∴. --1分 解得.. ∴AH=6. ∴AB=2AH=12, --1分 (3)P.A.O.C,A.B.D.C 或 P.A.O.D 或P.C.O.B.--2分(写对1个.2个.3个得1分.写对4个得2分)
网址：http://m.1010jiajiao.com/timu3_id_496131[举报]
如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与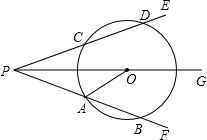
∠EPF的两边相交于A、B和C、D，连接OA，此时有OA∥PE．
（1）求证：AP=AO；
（2）若tan∠OPB=
，求弦AB的长；
（3）若以图中已标明的点（即P、A、B、C、D、O）构造四边形，则能构成菱形的四个点为 ，能构成等腰梯形的四个点为 或 或 ．
查看习题详情和答案>>
∠EPF的两边相交于A、B和C、D，连接OA，此时有OA∥PE．（1）求证：AP=AO；
（2）若tan∠OPB=
| 1 | 2 |
（3）若以图中已标明的点（即P、A、B、C、D、O）构造四边形，则能构成菱形的四个点为
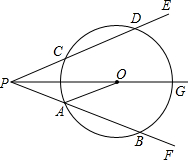如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心作⊙O，分别与∠EPF两边相交于A、B和C、D，连接OA，此时有OA∥PE．（1）求证：AP=AO；
（2）若以图中已标明的点（即P、A、B、C、D、O）构造四边形，那么请你直接写出能构成菱形的四边形和能构成等腰梯形的四边形（注意：不要漏掉呀！）．
（2011•金华）如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与∠EPF的两边相交于A、B和C、D，连接OA，此时有OA∥PE．
（1）求证：AP=AO；
（2）若tan∠OPB=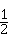
，求弦AB的长；
（3）若以图中已标明的点（即P、A、B、C、D、O）构造四边形，则能构成菱形的四个点为_________，能构成等腰梯形的四个点为__________或__________或___________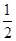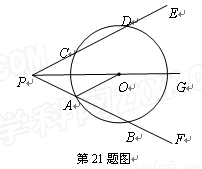
，求弦AB的长；
，求弦AB的长；