摘要: 如图.在平面直角坐标系中.点A.以OA为直径在第一象限内作半圆C.点B是该半圆周上的一动点.连结OB.AB.并延长AB至点D.使DB=AB.过点D作x轴垂线.分别交x轴.直线OB于点E.F.点E为垂足.连结CF. (1)当∠AOB=30°时.求弧AB的长, (2)当DE=8时.求线段EF的长, (3)在点B运动过程中.是否存在以点E.C.F为顶点的三角形与△AOB相似.若存在.请求出此时点E的坐标,若不存在.请说明理由. [解](1)连结BC. ∵A.∴OA=10.CA=5. ∵∠AOB=30°. ∴∠ACB=2∠AOB=60°. ∴的长==, (2)连结OD. ∵OA是⊙C的直径.∴∠OBA=90°. 又∵AB= BD. ∴OB是AD的垂直平分线. ∴OD= OA=10. 在Rt△ODE中. OE===6. ∴AE= AO-OE =10-6=4. 由∠AOB=∠ADE= 90°-∠OAB. ∠OEF=∠DEA. 得△OEF∽△DEA. ∴=.即=.∴EF=3, (3)设OE=x. ①当交点E在O.C之间时.由以点E.C.F为顶点的三角形与△AOB相似. 有∠ECF=∠BOA或∠ECF=∠OAB.当∠ECF=∠BOA时.此时△OCF为等腰三角形. 点E为OC的中点.即OE=. ∴E1(.0), 当∠ECF=∠OAB时.有CE=5-x.AE=10-x. ∴CF//AB.有CF=AB. ∵△ECF∽△EAD. ∴=.即=.解得x=. ∴E2(.0), ②当交点E在C的右侧时. ∵∠ECF>∠BOA ∴要使△ECF与△BAO相似.只能使∠ECF=∠BAO. 连结BE. ∵BE为Rt△ADE斜边上的中线. ∴BE=AB=BD. ∴∠BEA=∠BAO. ∴∠BEA=∠ECF. ∵CF//BE.∴=. ∵∠ECF=∠BAO.∠FEC=∠DEA=Rt∠. ∴△CEF∽△AED.∴=. 而AD=2BE.∴=. 即=. 解得x1=.x2=<0. ∴E3(.0), ③当交点E在O的左侧时. ∵∠BOA=∠EOF>∠ECF ∴要使△ECF与△BAO相似.只能使∠ECF=∠BAO. 连结BE.得BE=AD=AB. ∠BEA=∠BAO. ∴∠ECF=∠BEA. ∴CF//BE. ∴=. 又∵∠ECF=∠BAO.∠FEC=∠DEA=Rt∠. ∴△CEF∽△AED.∴=. 而AD=2BE.∴=. ∴=.解得x1=.x2=<0. ∵点E在x轴负半轴上.∴E4(.0). 综上所述:存在以点E.C.F为顶点的三角形与△AOB相似.此时点E坐标为: ∴E1(.0).E2(.0).E3(.0).E4(.0).
网址:http://m.1010jiajiao.com/timu3_id_496139[举报]
如图,在平面直角坐标系中,点A,B,C,P的坐标分别为(0,2),(3,2),(2,3),(1,1).
(1)请在图中画出△A′B′C′,使得△A′B′C′与△ABC关于点P成中心对称;
(2)若一个二次函数的图象经过(1)中△A′B′C′的三个顶点,求此二次函数的关系式.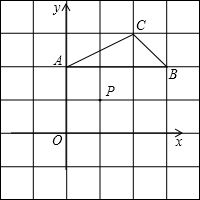 查看习题详情和答案>>
查看习题详情和答案>>
(1)请在图中画出△A′B′C′,使得△A′B′C′与△ABC关于点P成中心对称;
(2)若一个二次函数的图象经过(1)中△A′B′C′的三个顶点,求此二次函数的关系式.
 查看习题详情和答案>>
查看习题详情和答案>>
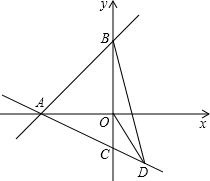
已知:如图,在平面直角坐标系中,0为坐标原点,直线y=x+3与x、y轴分别相交于点A、B,点C在y轴的负半轴上,且∠CAO=30°,点D在线段AC的延长线上,且CD=CO,连接OD、BD,BD交x轴于点E.
(1)求直线AC的解析式;
(2)求证:OB=OD;
(3)图中有几对相似三角形(不添加其他字母和线段)请写出所有的相似三角形,并选择其中的一对加以证明.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)求直线AC的解析式;
(2)求证:OB=OD;
(3)图中有几对相似三角形(不添加其他字母和线段)请写出所有的相似三角形,并选择其中的一对加以证明.
 查看习题详情和答案>>
查看习题详情和答案>>
 如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.(1)求tan∠BOA的值;
(2)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标;
(3)将△OAB平移得到△O′A′B′,点A的对应点是A′,点B的对应点B'的坐标为(2,-2),在坐标系中作出△O′A′B′,并写出点O′、A′的坐标. 查看习题详情和答案>>
 如图,在平面直角坐标系中,正方形ABCO的点A、C分别在x轴、y轴上,点B坐标为(6,6)连接AC.抛物线y=x2+bx+c经过B、C两点.
如图,在平面直角坐标系中,正方形ABCO的点A、C分别在x轴、y轴上,点B坐标为(6,6)连接AC.抛物线y=x2+bx+c经过B、C两点.(1)求抛物线的解析式.
(2)若动点E从原点出发,以每秒一个单位的速度,沿折线O-C-B-A做匀速运动,同时点F从原点出发,以相同的速度向x正半轴方向做匀速运动,过点E作ED⊥x轴于点D,当点E停止运动时,点F也停止运动.设△EFD的面积为S,运动时间为x(0<x<18),试写出S与x的函数关系式,并求出S的最大值.
(3)P是直线AC上的点,在抛物线上是否存在点Q,使以0、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
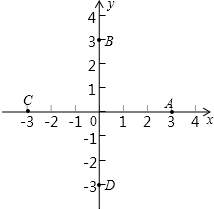 (2013•沙河口区一模)如图,在平面直角坐标系中,坐标是(0,-3)的点是( )
(2013•沙河口区一模)如图,在平面直角坐标系中,坐标是(0,-3)的点是( )