0 49559 49567 49573 49577 49583 49585 49589 49595 49597 49603 49609 49613 49615 49619 49625 49627 49633 49637 49639 49643 49645 49649 49651 49653 49654 49655 49657 49658 49659 49661 49663 49667 49669 49673 49675 49679 49685 49687 49693 49697 49699 49703 49709 49715 49717 49723 49727 49729 49735 49739 49745 49753 447348
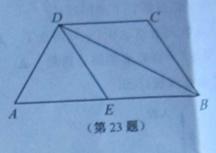
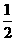 AB,BE=
AB,BE=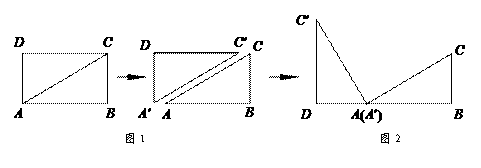


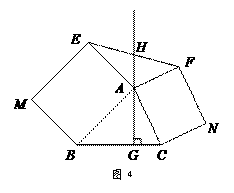




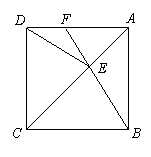
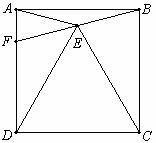
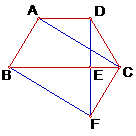
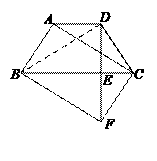
 沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=
沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=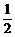 ∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.

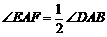 ,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).

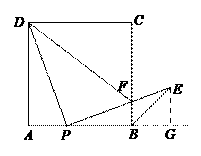
 ,将△ADE绕点A顺时针旋转
,将△ADE绕点A顺时针旋转 得到△ABG,此时AB与AD重合,由旋转可得:
得到△ABG,此时AB与AD重合,由旋转可得: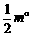 ∴∠2+∠3=∠BAD-∠EAF=
∴∠2+∠3=∠BAD-∠EAF=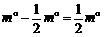


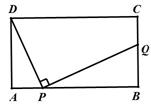
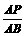 的值等于多少时,△PFD∽△BFP?并说明理由.
的值等于多少时,△PFD∽△BFP?并说明理由. 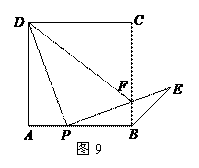

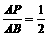 时,△PFE∽△BFP.·············································································· 6分
时,△PFE∽△BFP.·············································································· 6分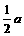 ,∴BF=BP·
,∴BF=BP·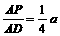 ···················· 8分
···················· 8分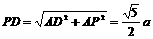 ,
,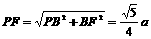
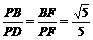 ··········································································································· 9分
··········································································································· 9分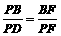 .·································································· 6分
.·································································· 6分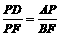 ,··············································································································· 8分
,··············································································································· 8分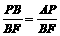 ,··············································································································· 9分
,··············································································································· 9分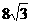 ,求AC的长.
,求AC的长.



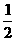 OC,设CF=
OC,设CF=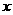 ,则OC= 2
,则OC= 2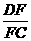 ∴DF=FC× tan 60°
∴DF=FC× tan 60°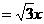
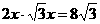 ,
, 

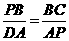 ,
,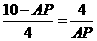 ,∴
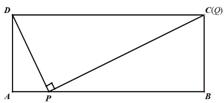
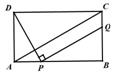
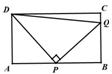
,∴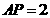 或8,∴存在点P使得点Q与点C重合,出此时AP的长2 或8.
或8,∴存在点P使得点Q与点C重合,出此时AP的长2 或8.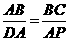 ,即
,即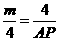 ,∴
,∴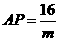 .
.
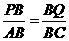 ,即
,即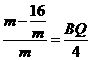 ,∴
,∴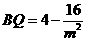 .
.
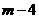 ,
,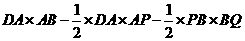
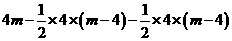 =16(4<
=16(4< ≤8).
≤8).

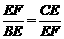 .
.