摘要： 已知:AB是⊙O的直径.弦CD⊥AB于点G.E是直线AB上一动点(不与点A.B.G重合).直线DE交⊙O于点F.直线CF交直线AB于点P.设⊙O的半径为r. (1)如图1.当点E在直径AB上时.试证明:OE·OP＝r2 (2)当点E在AB(或BA)的延长线上时.以如图2点E的位置为例.请你画出符合题意的图形.标注上字母.(1)中的结论是否成立?请说明理由. [答案](1)证明:连接FO并延长交⊙O于Q.连接DQ. ∵FQ是⊙O直径.∴∠FDQ＝90°. ∴∠QFD+∠Q＝90°. ∵CD⊥AB.∴∠P+∠C＝90°. ∵∠Q＝∠C.∴∠QFD＝∠P. ∵∠FOE＝∠POF.∴△FOE∽△POF. ∴.∴OE·OP＝OF2＝r2. 中的结论成立. 理由:如图2.依题意画出图形.连接FO并延长交⊙O于M.连接CM. ∵FM是⊙O直径.∴∠FCM＝90°.∴∠M+∠CFM＝90°. ∵CD⊥AB.∴∠E+∠D＝90°. ∵∠M＝∠D.∴∠CFM＝∠E. ∵∠POF＝∠FOE.∴△POF∽△FOE. ∴.∴OE·OP＝OF2＝r2.
网址：http://m.1010jiajiao.com/timu3_id_496135[举报]
（2011山东烟台，25，12分）
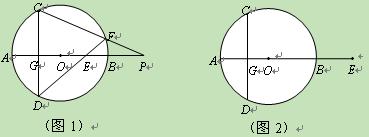
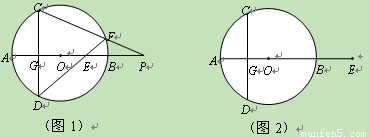
已知：AB是⊙O的直径，弦CD⊥AB于点G，E是直线AB上一动点（不与点A、B、G重合），直线DE交⊙O于点F，直线CF交直线AB于点P.设⊙O的半径为r.
（1）如图1，当点E在直径AB上时，试证明：OE·OP＝r2
（2）当点E在AB（或BA）的延长线上时，以如图2点E的位置为例，请你画出符合题意的图形，标注上字母，（1）中的结论是否成立？请说明理由.
查看习题详情和答案>>
（2011山东烟台，25，12分）
已知：AB是⊙O的直径，弦CD⊥AB于点G，E是直线AB上一动点（不与点A、B、G重合），直线DE交⊙O于点F，直线CF交直线AB于点P.设⊙O的半径为r.
（1）如图1，当点E在直径AB上时，试证明：OE·OP＝r2
（2）当点E在AB（或BA）的延长线上时，以如图2点E的位置为例，请你画出符合题意的图形，标注上字母，（1）中的结论是否成立？请说明理由.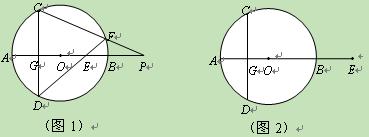
查看习题详情和答案>>
已知：AB是⊙O的直径，弦CD⊥AB于点G，E是直线AB上一动点（不与点A、B、G重合），直线DE交⊙O于点F，直线CF交直线AB于点P.设⊙O的半径为r.
（1）如图1，当点E在直径AB上时，试证明：OE·OP＝r2
（2）当点E在AB（或BA）的延长线上时，以如图2点E的位置为例，请你画出符合题意的图形，标注上字母，（1）中的结论是否成立？请说明理由.
查看习题详情和答案>>
