0 49443 49451 49457 49461 49467 49469 49473 49479 49481 49487 49493 49497 49499 49503 49509 49511 49517 49521 49523 49527 49529 49533 49535 49537 49538 49539 49541 49542 49543 49545 49547 49551 49553 49557 49559 49563 49569 49571 49577 49581 49583 49587 49593 49599 49601 49607 49611 49613 49619 49623 49629 49637 447348
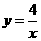 的图象,下列说法正确的是( )
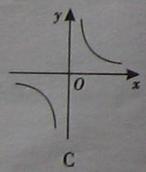
的图象,下列说法正确的是( )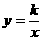 (k为常数,k≠0)的图像上,则这个反比例函数的大致图像是( )
(k为常数,k≠0)的图像上,则这个反比例函数的大致图像是( )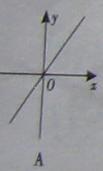
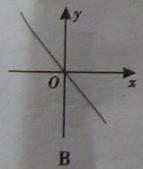
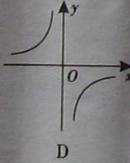
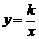 的图象经过(1,-2).则
的图象经过(1,-2).则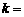 .
.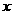 +n 相交于两点,这两点的坐标分别是(0,
+n 相交于两点,这两点的坐标分别是(0,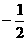 )和(m-b,m2
– mb + n,其中a,b,c,m,n为实数,且a,m不为0.
)和(m-b,m2
– mb + n,其中a,b,c,m,n为实数,且a,m不为0.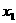 ,0)和(
,0)和(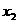 ,0),求
,0),求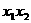 的值;
的值;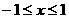 时,设抛物线y = ax2+bx+c与
时,设抛物线y = ax2+bx+c与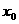 ,
,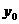 ),求这时
),求这时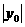 的最小值.
的最小值.
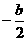 ,最小值为
,最小值为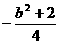 .(没写出不扣分)设抛物线y=x2+bx
.(没写出不扣分)设抛物线y=x2+bx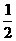 +b>
+b>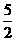 , (5分),在x轴下方与x轴距离最大的点是(-1,yo),∴|h|=|yo|=|
, (5分),在x轴下方与x轴距离最大的点是(-1,yo),∴|h|=|yo|=|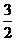 , (6分),∴|H|>|h|.∴这时|yo|的最小值大于
, (6分),∴|H|>|h|.∴这时|yo|的最小值大于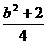 ≥
≥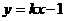 的图象平分它的面积,关于x的函数
的图象平分它的面积,关于x的函数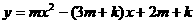 的图象与坐标轴只有两个交点,求m的值.
的图象与坐标轴只有两个交点,求m的值.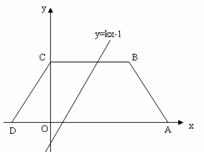
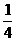 >0
>0 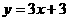 交
交 轴于B点,过A、B两点的抛物线交
轴于B点,过A、B两点的抛物线交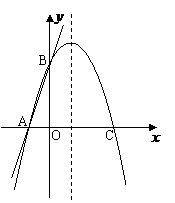

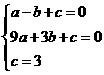 ,解得:
,解得: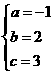 ,
,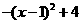 ,∴该抛物线的对称轴为x=1.
,∴该抛物线的对称轴为x=1.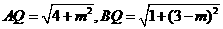 ,又
,又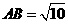 .
.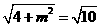 ,解得:
,解得: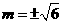 ,
,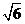 )或(1,
)或(1,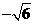 );
);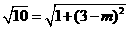 ,解得:
,解得: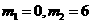 ,
,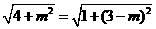 ,解得:
,解得: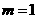 ,
,
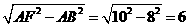 .
.
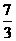 .
.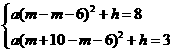 ,
,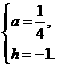
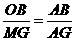 ,即
,即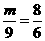 .
.

 x2 + bx-2上,∴
x2 + bx-2上,∴
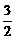 x-2. y=
x-2. y=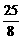 ,
,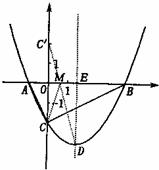
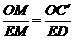
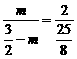 ,∴m =
,∴m =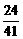 .
.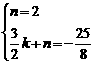 ,解得n =
2,
,解得n =
2, 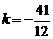 .
.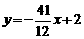 .
.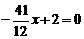 ,
,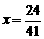 . ∴
. ∴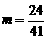 .
.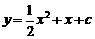 与x轴有两个不同的交点.
与x轴有两个不同的交点.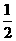
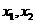 ,
,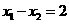 ,
,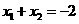
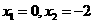
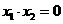
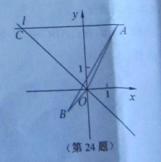
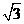 ,3),B(-1,-1),O(0,0),正比例y=-x的图象是直线l,直线AC∥x轴交直线l于点C.
,3),B(-1,-1),O(0,0),正比例y=-x的图象是直线l,直线AC∥x轴交直线l于点C.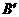 ,点A的对应点为
,点A的对应点为 ,得到△
,得到△ .
.
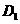 (9,-
(9,-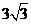 ),
), 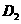 (
(