摘要:20.如图.等腰梯形ABCD的底边AD在x轴上.顶点C在y轴正半轴是.B(4,2).一次函数的图象平分它的面积.关于x的函数的图象与坐标轴只有两个交点.求m的值. 第22题图 [答案] 解:过B作BE⊥AD于E.连结OB.CE交于 点P. ∵P为矩形OCBE的对称中心.则过P点的直线平分矩形OCBE的面积. ∵P为OB的中点.而B 在Rt△ODC与Rt△EAB中.OC=BE.AB=CD ∴Rt△ODC≌Rt△EAB(HL). ∴S△ODC?=S△EBA? ∴过点的直线即可平分等腰梯形面积.这条直线为y=kx-1 ∴2k-1=1.∴k=1 又∵的图象与坐标轴只有两个交点.故 ①当m=0时.y=-x+1,其图象与坐标轴有两个交点 ②当m≠0时.函数的图象为抛物线.且与y轴总有一个交点 若抛物线过原点时.2m+1=0.即m=.此时△=2-4m=>0 ∴抛物线与x轴有两个交点且过原点.符合题意. 若抛物线不过原点.且与x轴只有一个交点.也合题意. 此时△′=2-4m=0 解之得:m1=m2=-1 综上所述.m的值为m=0或或-1.
网址:http://m.1010jiajiao.com/timu3_id_495406[举报]
如图,等腰梯形ABCD的BC边位于x轴上,A点位于y轴上,∠ABC=45°,BD平分AO(O为坐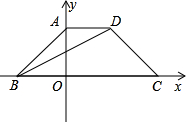 标原点),并且B(-1,0).
标原点),并且B(-1,0).
(1)求过点A、B、C的抛物线的解析式;
(2)P为(1)中抛物线上异于B的一点,过B、P两点的直线将梯形ABCD分成面积相等的两部分,求P点的坐标;
(3)在(1)中抛物线上是否存在点Q使△ABQ为直角三角形?若存在,求△ABQ的面积;若不存在,则说明理由. 查看习题详情和答案>>
 标原点),并且B(-1,0).
标原点),并且B(-1,0).(1)求过点A、B、C的抛物线的解析式;
(2)P为(1)中抛物线上异于B的一点,过B、P两点的直线将梯形ABCD分成面积相等的两部分,求P点的坐标;
(3)在(1)中抛物线上是否存在点Q使△ABQ为直角三角形?若存在,求△ABQ的面积;若不存在,则说明理由. 查看习题详情和答案>>
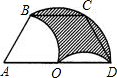 (2012•大兴区一模)如图,等腰梯形ABCD的上底BC长为1,弧OB、弧OD、弧BD的半径相等,弧OB弧BD所在圆的圆心分别为A、O.则图中阴影部分的面积
(2012•大兴区一模)如图,等腰梯形ABCD的上底BC长为1,弧OB、弧OD、弧BD的半径相等,弧OB弧BD所在圆的圆心分别为A、O.则图中阴影部分的面积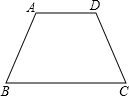 如图,等腰梯形ABCD的周长是104cm,AD∥BC,且AD:AB:BC=2:3:5,则这个梯形的中位线的长是( )
如图,等腰梯形ABCD的周长是104cm,AD∥BC,且AD:AB:BC=2:3:5,则这个梯形的中位线的长是( ) (2012•梁子湖区模拟)如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积,关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点,则m的值为( )
(2012•梁子湖区模拟)如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积,关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点,则m的值为( )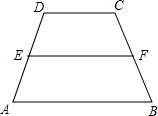 如图,等腰梯形ABCD的周长为18,腰AD=4,则等腰梯形ABCD的中位线EF=
如图,等腰梯形ABCD的周长为18,腰AD=4,则等腰梯形ABCD的中位线EF=