摘要： 如图(1).矩形ABCD的一边BC在直角坐标系中x轴上.折叠边AD,使点D落在x轴上点F处.折痕为AE.已知AB=8.AD=10.并设点B坐标为(m,0).其中m＞0. (1)求点E.F的坐标, (2)连接OA.若△OAF是等腰三角形.求m的值, .设抛物线y=a2+h经过A.E两点.其顶点为M.连接AM.若∠OAM=90°.求a.h.m的值. [答案]解:(1)∵四边形ABCD是矩形. ∴AD=BC=10.AB=CD=8.∠D=∠DCB=∠ABC=90°. 由折叠对称性:AF=AD=10.FE=DE. 在Rt△ABF中.BF=. ∴FC=4. 在Rt△ECF中.42+(8-x)2=x2.解得x=5. ∴CE=8-x=3. ∵B,F. (2)分三种情形讨论: 若AO=AF.∵AB⊥OF.∴OB=BF=6.∴m=6. 若OF=AF.则m+6=10.解得m=4. 若AO=OF.在Rt△AOB中.AO2=OB2+AB2=m2+64. ∴(m+6)2= m2+64.解得m=. 综合得m=6或4或. .E. 依题意.得. 解得 ∴M. 设对称轴交AD于G. ∴G.∴AG=6.GM=8-(﹣1)=9. ∵∠OAB+∠BAM=90°.∠BAM+∠MAG=90°. ∴∠OAB=∠MAG. 又∵∠ABO=∠MGA=90°. ∴△AOB∽△AMG. ∴.即. ∴m=12.
网址：http://m.1010jiajiao.com/timu3_id_495404[举报]
如图，矩形ABCD的一边AB=8cm，它的一条对角线AC=10cm，BE⊥AC于点E，则AE的长是（ ）
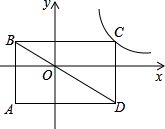（2013•新民市一模）如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y=| k2+2k+1 | x |
1或-3
1或-3
．（2013•湖州一模）如图①是矩形包书纸的示意图，虚线是折痕，四个角均为大小相同的正方形，正方形的边长为折叠进去的宽度．
（1）现有一本书长为25cm，宽为20cm，厚度是2cm，如果按照如图①的包书方式，并且折叠进去的宽度是3cm，则需要包书纸的长和宽分别为多少？（请直接写出答案）．
（2）已知数学课本长为26cm，宽为18.5cm，厚为1cm，小明用一张面积为1260cm2 的矩形包书纸按如图①包好了这本书，求折进去的宽度．
（3）如图②，矩形ABCD是一张一个角（△AEF）被污损的包书纸，已知AB=30，BC=50，AE=12，AF=16，要使用没有污损的部分包一本长为19，宽为16，厚为6的字典，小红认为只要按如图②的剪裁方式剪出一张面积最大的矩形PGCH就能包好这本字典．设PM=x，矩形PGCH的面积为y，当x取何值时y最大？并由此判断小红的想法是否可行．
查看习题详情和答案>>
（1）现有一本书长为25cm，宽为20cm，厚度是2cm，如果按照如图①的包书方式，并且折叠进去的宽度是3cm，则需要包书纸的长和宽分别为多少？（请直接写出答案）．
（2）已知数学课本长为26cm，宽为18.5cm，厚为1cm，小明用一张面积为1260cm2 的矩形包书纸按如图①包好了这本书，求折进去的宽度．
（3）如图②，矩形ABCD是一张一个角（△AEF）被污损的包书纸，已知AB=30，BC=50，AE=12，AF=16，要使用没有污损的部分包一本长为19，宽为16，厚为6的字典，小红认为只要按如图②的剪裁方式剪出一张面积最大的矩形PGCH就能包好这本字典．设PM=x，矩形PGCH的面积为y，当x取何值时y最大？并由此判断小红的想法是否可行．
如图，矩形ABCD的外接圆O与水平地面相切于A点，圆O半径为2，且
请将下面证明中每一步的理由填在括号内：