0 49510 49518 49524 49528 49534 49536 49540 49546 49548 49554 49560 49564 49566 49570 49576 49578 49584 49588 49590 49594 49596 49600 49602 49604 49605 49606 49608 49609 49610 49612 49614 49618 49620 49624 49626 49630 49636 49638 49644 49648 49650 49654 49660 49666 49668 49674 49678 49680 49686 49690 49696 49704 447348
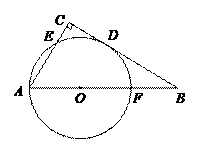
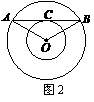
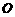 为圆心的两个同心圆中,大圆的弦
为圆心的两个同心圆中,大圆的弦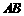 切小圆于点
切小圆于点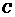 ,若
,若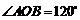 ,则大圆半径
,则大圆半径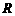 与小圆半径
与小圆半径 之间满足( )
之间满足( )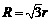 B.
B.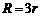 C.
C.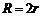 D.
D.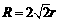
 是
是 上的三点,
上的三点,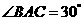 ,则
,则 度.
度.
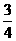 ,cos41°=
,cos41°=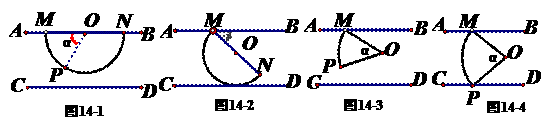
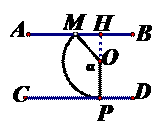
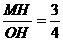 ,∴∠MOH=49°,∵α=2∠MOH,∴α最小值为98°。∴α的取值范围是98°≤α≤120°。
,∴∠MOH=49°,∵α=2∠MOH,∴α最小值为98°。∴α的取值范围是98°≤α≤120°。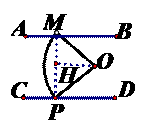
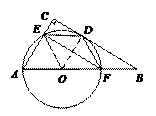
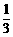 ,求DE的长.
,求DE的长.

 , 又∵AC = BC,
CD = CD, ∴
, 又∵AC = BC,
CD = CD, ∴ ≌
≌
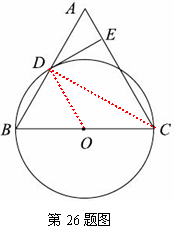
 ;
; 即DE是⊙O的切线;
即DE是⊙O的切线;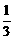 , ∵ cos∠B
=
, ∵ cos∠B
=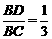 ,
BC = 18,
,
BC = 18,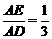 , ∴AE = 2,
, ∴AE = 2, 中,DE=
中,DE=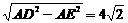 .
.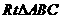 中,
中,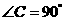 ,点D是AC的中点,且
,点D是AC的中点,且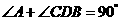 ,过点
,过点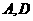 作
作 ,使圆心
,使圆心 在
在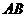 上,
上,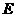 .
.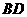 与
与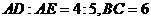 ,求
,求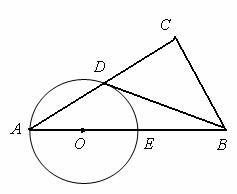
 中,OA=OD,
中,OA=OD,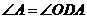 ,
,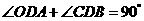 ,所以
,所以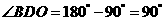 ,即
,即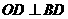 ,
,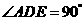 ,由题意可知
,由题意可知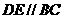 ,又点D是AC的中点,且
,又点D是AC的中点,且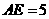 ,即
,即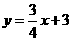 的图象是直线
的图象是直线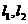 与x轴、y轴分别相交于A、B两点.直线
与x轴、y轴分别相交于A、B两点.直线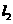 过点C(a,0)且与
过点C(a,0)且与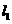 垂直,其中a>0,点P、Q同时从A点出发,其中点P沿射线AB运动,速度为每秒4个单位;点Q沿射线AO运动,速度为每秒5个单位.
垂直,其中a>0,点P、Q同时从A点出发,其中点P沿射线AB运动,速度为每秒4个单位;点Q沿射线AO运动,速度为每秒5个单位.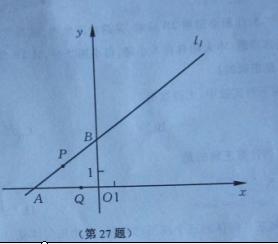
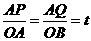 ,又∠PAQ=∠QAB,∴△APQ∽△AOB.
,又∠PAQ=∠QAB,∴△APQ∽△AOB.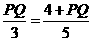 ,∴PQ=6,
,∴PQ=6,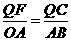 .
.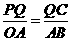 ,
,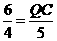 ,∴QC=
,∴QC=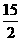 ,a=OQ+QC=
,a=OQ+QC=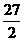 .
.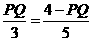 ,∴PQ=
,∴PQ=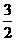 .
.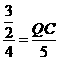 ,
,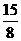 ,a=QC-OQ=
,a=QC-OQ=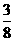 .∴a的值为
.∴a的值为