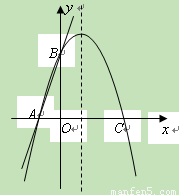
摘要: (2011湖南湘潭市.25.10分) 如图.直线交轴于A点.交轴于B点.过A.B两点的抛物线交轴于另一点C(3,0). ⑴ 求抛物线的解析式; ⑵ 在抛物线的对称轴上是否存在点Q.使△ABQ是等腰三角形?若存在.求出符合条件的Q点坐标,若不存在.请说明理由. [答案]解:(1)设抛物线的解析式为:y=ax2+bx+c. ∵直线交轴于A点.交轴于B点. ∴A点坐标为. 又∵抛物线经过A.B.C三点. ∴.解得:. ∴抛物线的解析式为:y=-x2+2x+3. (2)∵y=-x2+2x+3= .∴该抛物线的对称轴为x=1. 设Q点坐标为(1.m).则.又. 当AB=AQ时. .解得:. ∴Q点坐标为(1.)或(1.), 当AB=BQ时..解得:. ∴Q点坐标为, 当AQ=BQ时..解得:. ∴Q点坐标为(1.1). ∴抛物线的对称轴上是存在着点Q(1.).(1.)..使△ABQ是等腰三角形.
网址:http://m.1010jiajiao.com/timu3_id_495405[举报]
(本题满分10分)如图,直线 交
交 轴于A点,交
轴于A点,交 轴于B点,过A、B两点的抛物线交
轴于B点,过A、B两点的抛物线交 轴于另一点C(3,0)
轴于另一点C(3,0) .
.
⑴求抛物线的解析式;
⑵在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
 交
交 轴于A点,交
轴于A点,交 轴于B点,过A、B两点的抛物线交
轴于B点,过A、B两点的抛物线交 轴于另一点C(3,0)
轴于另一点C(3,0) .
. ⑴求抛物线的解析式;
⑵在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.

(本小题12分)如图,直线![]() 交
交![]() 轴于A点,交
轴于A点,交![]() 轴于B点,过A、B两点的抛物线交
轴于B点,过A、B两点的抛物线交![]() 轴于另一点C(3,0).
轴于另一点C(3,0).

1.⑴ 求抛物线的解析式;
2.⑵ 在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
查看习题详情和答案>>
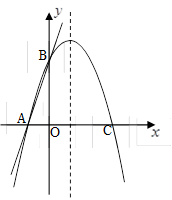
(本小题满分12分)如图,直线交
轴于A点,交
轴于B点,过A、B两点的抛物线交
轴于另一点C(3,0).
⑴ 求抛物线的解析式;
⑵ 在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
查看习题详情和答案>>
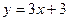 交
交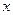 轴于A点,交
轴于A点,交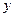 轴于B点,过A、B两点的抛物线交
轴于B点,过A、B两点的抛物线交
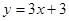 交
交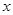 轴于A点,交
轴于A点,交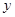 轴于B点,过A、B两点的抛物线交
轴于B点,过A、B两点的抛物线交