23.(本题10分)某班实行小组量化考核制.为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:
综合评价得分统计表 (单位:分)

(1)请根据表中的数据完成下表(注:方差的计算结果精确到0.1)
解:
|
|
平均数 |
中位数 |
方差 |
|
甲组 |
14 |
14 |
1.7 |
|
乙组 |
14 |
15 |
11.7 |
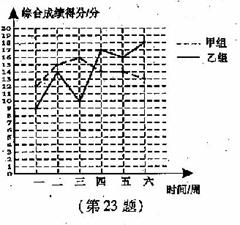
(2)根据综合评价得分统计表中的数据,请在下图中画出乙组综合评价得分的折线统计图.
解:折线图如右图.
(3)根据折线统计图中的信息,请你分别对甲、乙两个小组连续六周的学习情况作出简要评价.
解:从折线图可看出:甲组戚绩相对稳定,但进步不大,且略有下降趋势.
乙组成绩不够稳定,但进步较快,呈上升趋势.
评分说明:答案不唯一,只要符合题意即可得分.
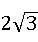 D、
D、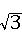
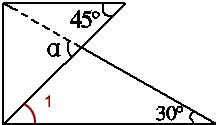
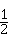 ∠CBA=30°,
∠CBA=30°,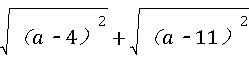 化简后为( )
化简后为( )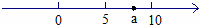
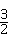 的倒数是( )
的倒数是( )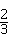
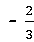 )=1,,
)=1,,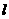 经过O、C两点.点A的坐标为(8,o),点B的坐标为(11.4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单
经过O、C两点.点A的坐标为(8,o),点B的坐标为(11.4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单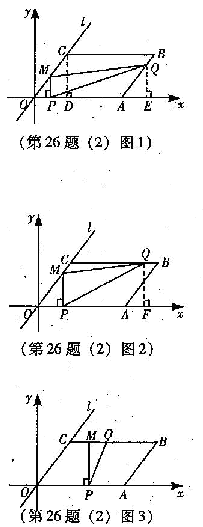 位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C-B相交于点M。当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P、Q运动的时间为t秒(
位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C-B相交于点M。当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P、Q运动的时间为t秒(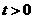 ).△MPQ的面积为S.
).△MPQ的面积为S.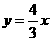
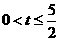 时,如图l,M点的坐标是(
时,如图l,M点的坐标是(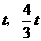 ).
).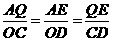 ,∴
,∴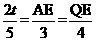 ,∴
,∴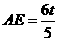 ,
,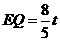
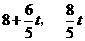 ),∴PE=
),∴PE=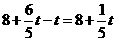
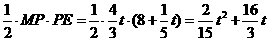
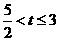 时,如图2,过点q作QF⊥x轴于F,
时,如图2,过点q作QF⊥x轴于F,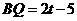 ,∴OF=
,∴OF=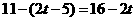
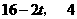 ),∴PF=
),∴PF=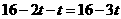
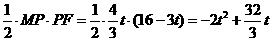
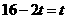 ,解得
,解得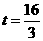 。
。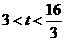 时,如图3,MQ=
时,如图3,MQ=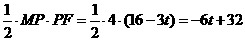
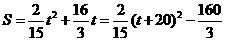
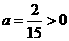 ,抛物线开口向上,对称轴为直线
,抛物线开口向上,对称轴为直线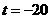 ,
,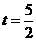 时,S有最大值,最大值为
时,S有最大值,最大值为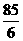 .
.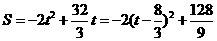 。∵
。∵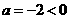 ,抛物线开口向下.
,抛物线开口向下.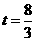 时,S有最大值,最大值为
时,S有最大值,最大值为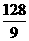 .
. 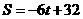 ,∵
,∵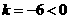 .∴S随t的增大而减小.
.∴S随t的增大而减小.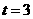 时,S=14.当
时,S=14.当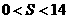 .
.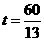 时,△QMN为等腰三角形.
时,△QMN为等腰三角形.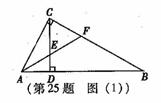 (1)求证:CE=CF.
(1)求证:CE=CF.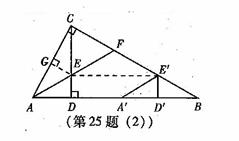 (2)将图(1)中的△ADE沿AB向右平移到△A’D’E’的位置,使点E’落在BC边上,其它条
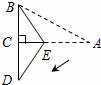
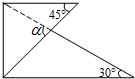
(2)将图(1)中的△ADE沿AB向右平移到△A’D’E’的位置,使点E’落在BC边上,其它条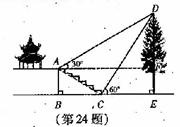 (本题7分)如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度.他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2米,台阶AC的坡度为
(本题7分)如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度.他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2米,台阶AC的坡度为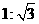 (即AB:BC=
(即AB:BC=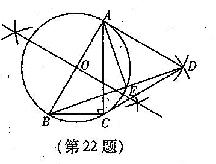 ①作△ABC的外接圆,圆心为O;
①作△ABC的外接圆,圆心为O;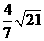 或
或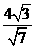 )
)