0 49653 49661 49667 49671 49677 49679 49683 49689 49691 49697 49703 49707 49709 49713 49719 49721 49727 49731 49733 49737 49739 49743 49745 49747 49748 49749 49751 49752 49753 49755 49757 49761 49763 49767 49769 49773 49779 49781 49787 49791 49793 49797 49803 49809 49811 49817 49821 49823 49829 49833 49839 49847 447348
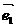 、
、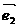 是平面上的一组基底,则下列各组向量中不能作为基底的一组是 ( )
是平面上的一组基底,则下列各组向量中不能作为基底的一组是 ( )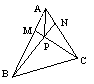 答案:D
答案:D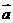 = (3,-4)平行的单位向量是_________;
= (3,-4)平行的单位向量是_________;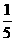
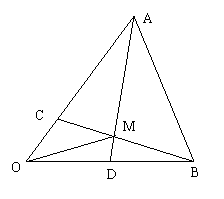
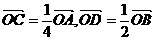 ,AD与BC交于点M,设
,AD与BC交于点M,设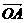 =
=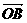 =
=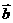 ,用
,用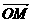 .
.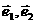 是一个平面内的两个不共线向量,则根据平面向量的基本定理,平面内的任何向量都可用
是一个平面内的两个不共线向量,则根据平面向量的基本定理,平面内的任何向量都可用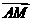 与
与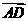 共线,向量
共线,向量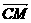 与
与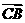 共线,建立关于m,n的两个方程.
共线,建立关于m,n的两个方程.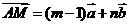 ,
,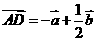

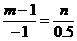 ,∴m+2n=1. ①
,∴m+2n=1. ① 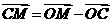
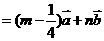 ,
,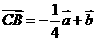
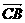 共线,
共线,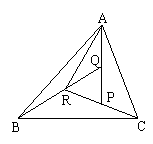 ∴
∴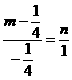 ,∴4m+n=1. ②
,∴4m+n=1. ② 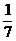 ,n=
,n=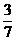 ,∴
,∴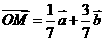
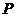 是
是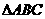 所在平面内一点,
所在平面内一点,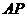 的中点为
的中点为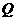 ,
,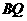 的中点为
的中点为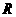 ,
, 的中点为
的中点为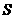 .证明:只有唯一的一点
.证明:只有唯一的一点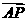 可用一组基底唯一表示.
可用一组基底唯一表示.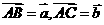 ,
,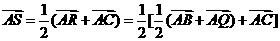
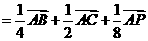 ,
,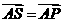
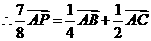
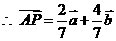
 =(x1, y1) ,
=(x1, y1) ,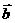 =(x2, y2) 其中
=(x2, y2) 其中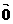 )的充要条件是
)的充要条件是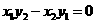
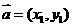 ,
,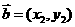 ,则
,则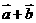 =
=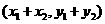 ,
,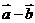 =
= 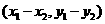

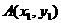 ,
,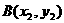 ,则
,则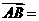
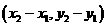
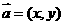 和实数
和实数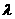 ,则
,则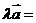
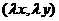
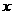 轴、
轴、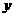 轴方向相同的两个__单位向量_
轴方向相同的两个__单位向量_ 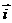 、
、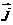 作为基底
作为基底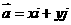 …………1,
…………1,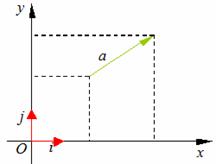
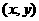 叫做向量
叫做向量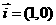 ,
,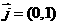 ,
,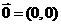
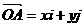 ,则向量
,则向量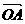 的坐标
的坐标 的坐标;反过来,点
的坐标;反过来,点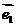 、
、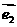 叫做表示这一平面内所有向量的一组基底;
叫做表示这一平面内所有向量的一组基底;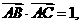
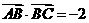 .
. 证明:
证明: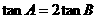 ;
;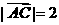 ,求
,求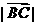 .
.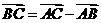 ∴
∴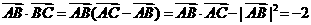
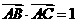 ∴
∴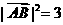 ,
, 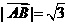 即AB边的长度为
即AB边的长度为 ----------------4分
----------------4分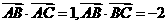 得
得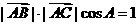 --------------------①
--------------------①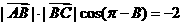 即
即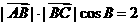 --------------------②-----6分
--------------------②-----6分 由①②得
由①②得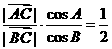 , 由正弦定理得
, 由正弦定理得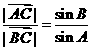
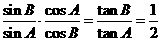
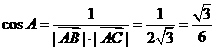
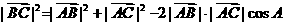 =
=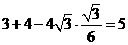
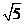 --------------------------------------------------------------------------14分
--------------------------------------------------------------------------14分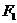 、
、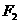 分别是椭圆
分别是椭圆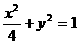 的左、右焦点.若
的左、右焦点.若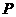 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求
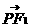 ·
·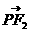 的最大值和最小值;
的最大值和最小值;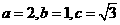 ,所以
,所以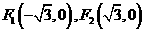
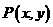 ,则
,则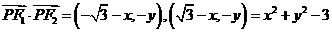
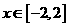 ,故当
,故当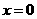 ,即点
,即点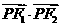 有最小值
有最小值
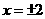 ,即点
,即点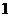
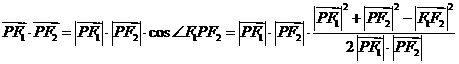
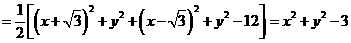 …
…