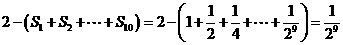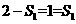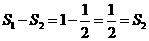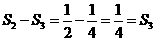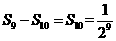6. (2011浙江绍兴,23,12分)数学课上,李老师出示了如下框中的题目.
小敏与同桌小聪讨论后,进行了如下解答:
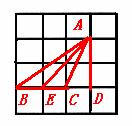
(1)特殊情况,探索结论
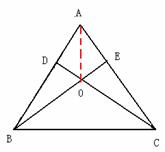
当点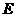 为
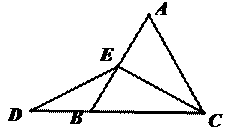
为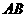 的中点时,如图1,确定线段
的中点时,如图1,确定线段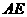 与
与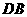 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论:
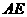
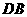 (填“>”,“<”或“=”).
(填“>”,“<”或“=”).
|
|
(2)特例启发,解答题目
解:题目中,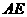 与
与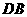 的大小关系是:
的大小关系是: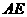
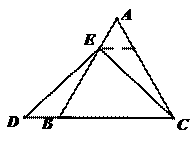
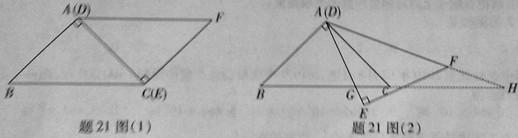
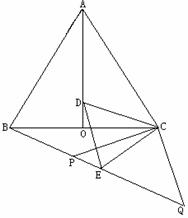
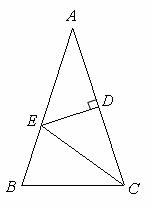
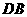 (填“>”,“<”或“=”).理由如下:如图2,过点
(填“>”,“<”或“=”).理由如下:如图2,过点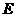 作
作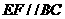 ,交
,交 于点
于点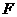 .
.
(请你完成以下解答过程)
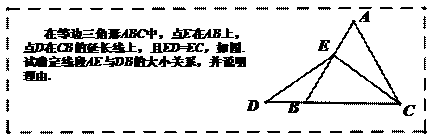
(3)拓展结论,设计新题
在等边三角形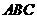 中,点
中,点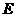 在直线
在直线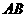 上,点
上,点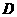 在直线
在直线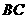 上,且
上,且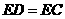 .若
.若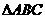 的边长为1,
的边长为1,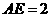 ,求
,求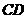 的长(请你直接写出结果).
的长(请你直接写出结果).
[答案](1)= .
(2)=.
方法一:如图,等边三角形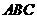 中,
中,
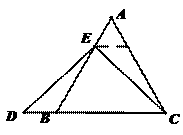
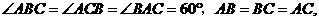
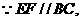
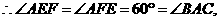
 是等边三角形,
是等边三角形,
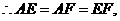
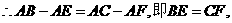
又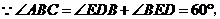
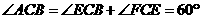
.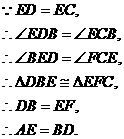
方法二:在等边三角形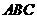 中,
中,

而由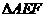 是正三角形可得
是正三角形可得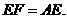
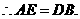
(3)1或3.
 ③;①③
③;①③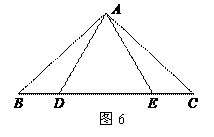



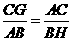 ,即
,即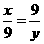 ,
,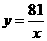
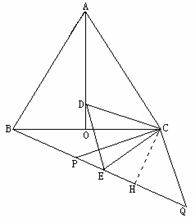
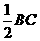 时,∠GAC=∠H<∠HAC,∴AC<CH
时,∠GAC=∠H<∠HAC,∴AC<CH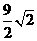 ,即x=
,即x=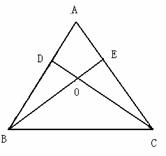
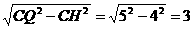



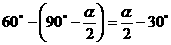
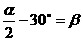 即α=2β+60°
即α=2β+60° 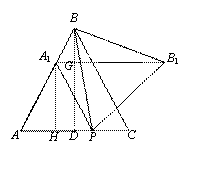

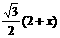 在Rt△ABD中,BD=
在Rt△ABD中,BD=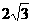
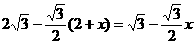
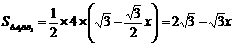 (0≤x<2)
(0≤x<2)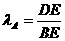 。特别的,当点D重合时,规定
。特别的,当点D重合时,规定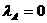 。另外。对
。另外。对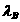 、
、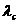 作类似的规定。
作类似的规定。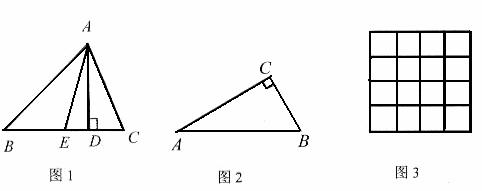
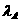 、
、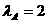 ,面积也为2;
,面积也为2;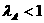 ,则△ABC为锐角三角形;( )
,则△ABC为锐角三角形;( )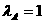 ,则△ABC为直角三角形;( )
,则△ABC为直角三角形;( )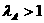 ,则△ABC为钝角三角形;( )
,则△ABC为钝角三角形;( )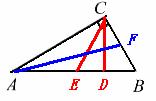
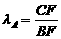 =1
=1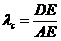 =
=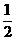 ; ∴
; ∴
 .
.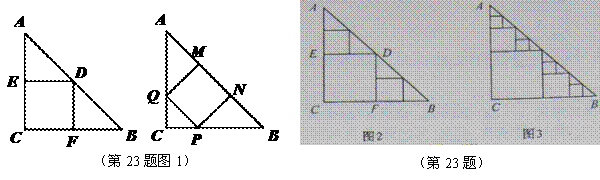

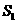 ;按照甲种剪法,在余下的
;按照甲种剪法,在余下的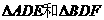 中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为
中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为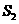 (如图2),则
(如图2),则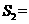 ;再在余下的四个三角形中,用同样的方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形的面积和为
;再在余下的四个三角形中,用同样的方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形的面积和为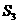 (如图3);继续操作下去…则第10次剪取时,
(如图3);继续操作下去…则第10次剪取时,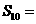 .
. 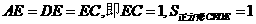 .如图乙,设
.如图乙,设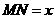 ,则由题意,得
,则由题意,得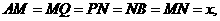

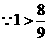
 甲种剪法所得的正方形的面积更大
甲种剪法所得的正方形的面积更大 的中点,
的中点,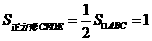
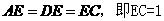
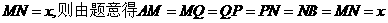
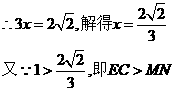
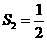
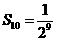
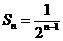 ‘
‘