摘要: 是一张等腰直角三角形纸板.. 要在这张纸板中剪出一个尽可能大的正方形.有甲.乙两种剪法.比较甲.乙两种剪法.哪种剪法所得的正方形面积更大?请说明理由. 图1中甲种剪法称为第1次剪取.记所得的正方形面积为,按照甲种剪法.在余下的中.分别剪取正方形.得到两个相同的正方形.称为第2次剪取.并记这两个正方形面积和为.则 ,再在余下的四个三角形中.用同样的方法分别剪取正方形.得到四个相同的正方形.称为第3次剪取.并记这四个正方形的面积和为,继续操作下去-则第10次剪取时. . 求第10次剪取后.余下的所有小三角形的面积和. [答案](1)解法1:如图甲.由题意得.如图乙.设.则由题意.得 又 甲种剪法所得的正方形的面积更大 说明:图甲可另解为:由题意得点D.E.F分别为的中点. 解法2:如图甲.由题意得 如图乙.设 甲种剪法所得的正方形的面积更大 (2) (3) (3)解法1:探索规律可知:` 剩余三角形的面积和为: 解法2:由题意可知. 第一次剪取后剩余三角形面积和为 第二次剪取后剩余三角形面积和为 第三次剪取后剩余三角形面积和为 - 第十次剪取后剩余三角形面积和为
网址:http://m.1010jiajiao.com/timu3_id_496621[举报]
 如图△ABC是一张等腰直角三角形彩色纸,AC=BC=20cm.将斜边上的高CD五等分,然后裁出4张宽度相等的长方形纸条.这4张小长方形的面积和
如图△ABC是一张等腰直角三角形彩色纸,AC=BC=20cm.将斜边上的高CD五等分,然后裁出4张宽度相等的长方形纸条.这4张小长方形的面积和160
160
cm2.若将这个等腰直角三角形的斜边上的高n等分,那么这些n-1个小长方形的面积和是200-
| 200 |
| n |
200-
cm2.| 200 |
| n |
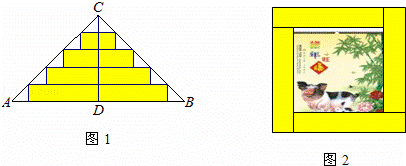
如图1,△ABC是一张等腰直角三角形彩色纸,AC=BC=50cm.将斜边上的高CD五等分,然后裁出4张宽度相等的长方形纸条.若用这4张纸条为一幅正方形美术作品镶边(纸条不重叠),如图2,则正方形美术作品最大面积是

查看习题详情和答案>>
800
800
cm2.
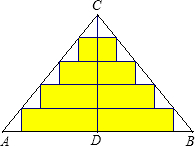 如图,△ABC是一张等腰直角三角形彩色纸,AC=BC=40cm.
如图,△ABC是一张等腰直角三角形彩色纸,AC=BC=40cm.问题1:将斜边上的高CD五等分,然后裁出4张宽度相等的长方形纸条.则这4张纸条的面积和是
问题2:若将斜边上的高CD n等分,然后裁出(n-1)张宽度相等的长方形纸条.则这(n-1)张纸条的面积和是
 如图△ABC是一张等腰直角三角形彩色纸,AC=BC=20cm.将斜边上的高CD五等分,然后裁出4张宽度相等的长方形纸条.这4张小长方形的面积和________cm2.若将这个等腰直角三角形的斜边上的高n等分,那么这些n-1个小长方形的面积和是________cm2.
如图△ABC是一张等腰直角三角形彩色纸,AC=BC=20cm.将斜边上的高CD五等分,然后裁出4张宽度相等的长方形纸条.这4张小长方形的面积和________cm2.若将这个等腰直角三角形的斜边上的高n等分,那么这些n-1个小长方形的面积和是________cm2.