摘要: 如图1.在等边△ABC中.点D是边AC的中点.点P是线段DC上的动点(点P与点C不重合).连结BP. 将△ABP绕点P按顺时针方向旋转α角(0°<α<180°).得到△A1B1P,连结AA1.射线AA1分别交射线PB.射线B1B于点E.F. (1) 如图1.当0°<α<60°时.在α角变化过程中.△BEF与△AEP始终存在 ▲ 关系.并说明理由, (2)如图2.设∠ABP=β . 当60°<α<180°时.在α角变化过程中.是否存在△BEF与△AEP全等?若存在.求出α与β之间的数量关系,若不存在.请说明理由, (3)如图3.当α=60°时.点E.F与点B重合. 已知AB=4.设DP=x.△A1BB1的面 积为S.求S关于x的函数关系 [答案](1) 相似 由题意得:∠APA1=∠BPB1=α AP= A1P BP=B1P 则 ∠PAA1 =∠PBB1 = ∵∠PBB1 =∠EBF ∴∠PAE=∠EBF 又∵∠BEF=∠AEP ∴△BEF ∽△AEP (2)存在.理由如下: 易得:△BEF ∽△AEP 若要使得△BEF≌△AEP.只需要满足BE=AE即可 ∴∠BAE=∠ABE ∵∠BAC=60° ∴∠BAE= ∵∠ABE=β ∠BAE=∠ABE ∴ 即α=2β+60° (3)连结BD.交A1B1于点G. 过点A1作A1H⊥AC于点H. ∵∠B1 A1P=∠A1PA=60° ∴A1B1∥AC 由题意得:AP= A1 P ∠A=60° ∴△PAA1是等边三角形 ∴A1H=在Rt△ABD中.BD= ∴BG= ∴ (0≤x<2)
网址:http://m.1010jiajiao.com/timu3_id_496624[举报]
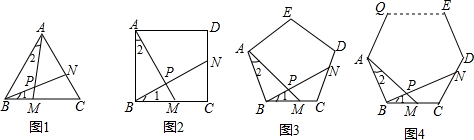
(1)如图1,在等边△ABC中,∠1=∠2,求∠APN的度数;
(2)如图2,在正方形ABCD中,∠1=∠2,则∠APN=
如图3,在正五边形ABCDE中,∠1=∠2,则∠APN=
(3)如图4,在正n边形ABCDE…Q中,∠1=∠2,则∠APN=
.(用含有n的式子表示)
查看习题详情和答案>>
(2)如图2,在正方形ABCD中,∠1=∠2,则∠APN=
60°
60°
;如图3,在正五边形ABCDE中,∠1=∠2,则∠APN=
90°
90°
;(3)如图4,在正n边形ABCDE…Q中,∠1=∠2,则∠APN=
| (n-2)180° |
| n |
| (n-2)180° |
| n |

(1)画图探究:
如图1,若点A、B在直线m同侧,在直线m上求作一点P,使AP+BP的值最小,保留作图痕迹,不写作法;
(2)实践运用:
如图2,在等边△ABC中,AB=2,点E是AB的中点,AD是高,点P是高AD上一个动点,求BP+PE的最小值
(3)拓展延伸:
如图3,四边形ABCD中,∠BAD=125°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小,并求此时∠MAN的度数.

查看习题详情和答案>>
如图1,若点A、B在直线m同侧,在直线m上求作一点P,使AP+BP的值最小,保留作图痕迹,不写作法;
(2)实践运用:
如图2,在等边△ABC中,AB=2,点E是AB的中点,AD是高,点P是高AD上一个动点,求BP+PE的最小值
(3)拓展延伸:
如图3,四边形ABCD中,∠BAD=125°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小,并求此时∠MAN的度数.

15、已知,E、F分别是正多边形相邻两边上的点,且CE=BF,AF交BE于P,如图1,在等边△ABC中,有∠EPA=60°;如图2,在正方形ABCD中,有∠EPA=90°;如图3在正五边形ABCDM中,有∠EPA=108°;依此规律,在正八边形中,有∠EPA=

查看习题详情和答案>>
135
度.
(2013•衢州)【提出问题】
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.

查看习题详情和答案>>
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.

(2013•宜兴市二模)阅读下面材料:
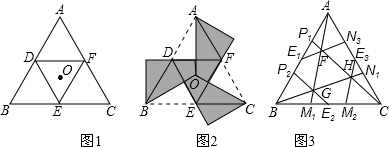
小明同学遇到这样一个问题:定义:如果一个图形绕着某定点旋转一定的角度α (0°<α<360°) 后所得的图形与原图形重合,则称此图形是旋转对称图形.如等边三角形就是一个旋转角为120°的旋转对称图形.如图1,点O是等边三角形△ABC的中心,D、E、F分别为AB、BC、CA的中点,请你将△ABC分割并拼补成一个与△ABC面积相等的新的旋转对称图形.小明利用旋转解决了这个问题(如图2所示).图2中阴影部分所示的图形即是与△ABC面积相等的新的旋转对称图形.请你参考小明同学解决问题的方法,利用图形变换解决下列问题:
如图3,在等边△ABC中,E1、E2、E3分别为AB、BC、CA 的中点,P 1、P2,M1、M2,N1、N2分别为AB、BC、CA的三等分点.
(1)在图3中画-个和△ABC面积相等的新的旋转对称图形,并用阴影表示(保留画图痕迹);
(2)若△ABC的边长为6,则图3中△ABM1的面积为
(3)若△ABC的面积为a,则图3中△FGH的面积为
.
查看习题详情和答案>>
小明同学遇到这样一个问题:定义:如果一个图形绕着某定点旋转一定的角度α (0°<α<360°) 后所得的图形与原图形重合,则称此图形是旋转对称图形.如等边三角形就是一个旋转角为120°的旋转对称图形.如图1,点O是等边三角形△ABC的中心,D、E、F分别为AB、BC、CA的中点,请你将△ABC分割并拼补成一个与△ABC面积相等的新的旋转对称图形.小明利用旋转解决了这个问题(如图2所示).图2中阴影部分所示的图形即是与△ABC面积相等的新的旋转对称图形.请你参考小明同学解决问题的方法,利用图形变换解决下列问题:
如图3,在等边△ABC中,E1、E2、E3分别为AB、BC、CA 的中点,P 1、P2,M1、M2,N1、N2分别为AB、BC、CA的三等分点.
(1)在图3中画-个和△ABC面积相等的新的旋转对称图形,并用阴影表示(保留画图痕迹);
(2)若△ABC的边长为6,则图3中△ABM1的面积为
3
| 3 |
3
.| 3 |
(3)若△ABC的面积为a,则图3中△FGH的面积为
| a |
| 7 |
| a |
| 7 |
