摘要: 如图. △ABC中.AB=AC.∠A=36°.AC的垂直平分线交AB于E.D为垂足.连结EC. (1)求∠ECD的度数, (2)若CE=5.求BC长. [答案](1)解法一:∵DE垂直平分AC.∴CE=AE.∠ECD=∠A=36°. 解法二:∵DE垂直平分AC.∴AD=CD.∠ADE=∠CDE=90°. 又∵DE =DE.∴△ADE≌△CDE.∠ECD=∠A=36°. (2)解法一:∵AB=AC.∠A=36°.∴∠B=∠ACB=72°. ∵∠ECD=36°. ∴∠BCE=∠ACB-∠ECD=36°. ∠BEC=72°=∠B. ∴ BC=EC=5. 解法二:∵AB=AC.∠A=36°. ∴∠B=∠ACB=72°. ∴∠BEC=∠A+∠ECD=72°. ∴∠BEC=∠B. ∴BC=EC=5.
网址:http://m.1010jiajiao.com/timu3_id_496625[举报]
 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.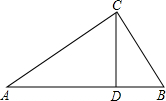 如图,△ABC中,CD是边AB上的高,且
如图,△ABC中,CD是边AB上的高,且 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )