0 49546 49554 49560 49564 49570 49572 49576 49582 49584 49590 49596 49600 49602 49606 49612 49614 49620 49624 49626 49630 49632 49636 49638 49640 49641 49642 49644 49645 49646 49648 49650 49654 49656 49660 49662 49666 49672 49674 49680 49684 49686 49690 49696 49702 49704 49710 49714 49716 49722 49726 49732 49740 447348
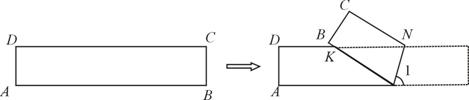
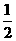 ?若能,求出此时∠1的度数;若不能,试说明理由.
?若能,求出此时∠1的度数;若不能,试说明理由.
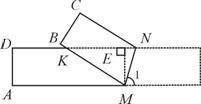 ∴AM∥DN,
∴AM∥DN,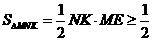 .
.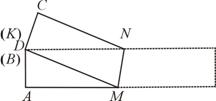
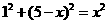 ,
,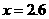 .
.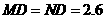 .
.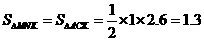 .
(情况一)
.
(情况一)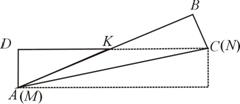 情况二:将矩形纸片沿对角线AC对折,此时折痕为AC.
情况二:将矩形纸片沿对角线AC对折,此时折痕为AC.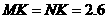 .
.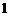 ,正方形
,正方形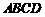 的边长为
的边长为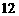 ,
, 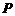 为边
为边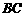 延长线上的一点,
延长线上的一点,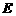 为
为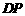 的中点,
的中点, 于
于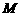 ,交边
,交边 的延长线于
的延长线于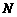 .当
.当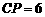 时,
时, 与
与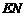 的比值是多少?
的比值是多少?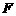 ,
,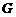 ,如图
,如图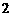 ,则可得:
,则可得: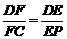 ,因为
,因为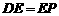 ,所以
,所以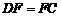 .可求出
.可求出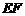 和
和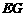 的值,进而可求得
的值,进而可求得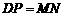 的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.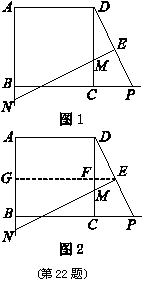

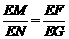 ,
,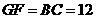 .
.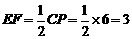 ,
,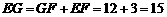 .
.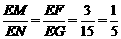 . ··················· 4分
. ··················· 4分 ∥
∥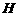 ,················ 5分
,················ 5分 ,
,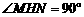 .
.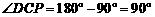 ,
,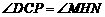 .
.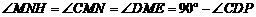 ,
,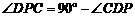 ,
,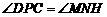 .∴
.∴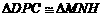 .··········· 7分
.··········· 7分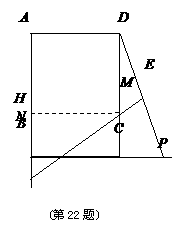


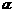 ,测出飞机在B处对山顶的俯角为
,测出飞机在B处对山顶的俯角为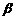 ,测出AB的距离为d,连接AM,BM.
,测出AB的距离为d,连接AM,BM.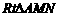 中,
中,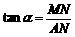 ∴
∴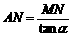
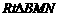 中,
中,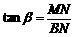 ∴
∴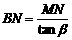
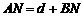 ,解得
,解得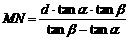 .
.
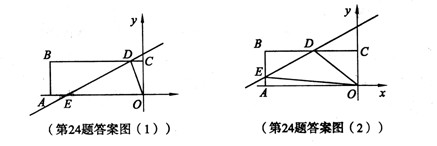
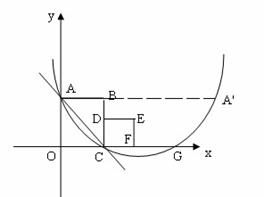
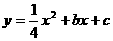 经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.
经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.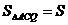 ,直接写出s与t之间的函数关系式.
,直接写出s与t之间的函数关系式.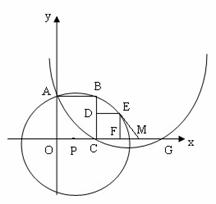
 (舍去)
(舍去)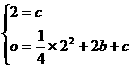 ,解之得:
,解之得: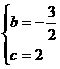
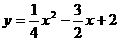 ?
?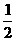 FG=
FG=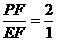 ,
,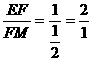
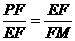 ,而∠PFE=∠FEM=90°
,而∠PFE=∠FEM=90°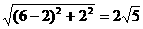 ,
,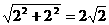
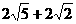
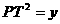 ,
,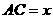 ,求
,求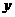 与
与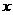 的函数关系式及
的函数关系式及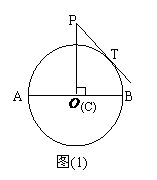

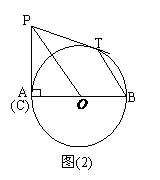

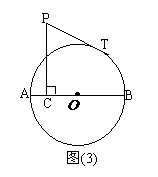

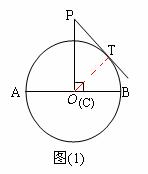
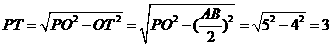 .
.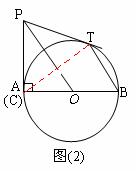
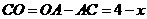 .
.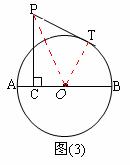
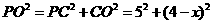
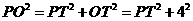 ,
,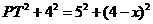 ,即
,即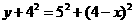 .
.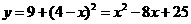 .
.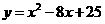 ,
,  中,把抛物线
中,把抛物线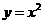 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线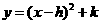 .所得抛物线与
.所得抛物线与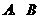 两点(点
两点(点 在点
在点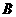 的左边),与
的左边),与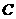 ,顶点为
,顶点为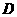 .
.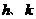 的值;
的值; 的形状,并说明理由;
的形状,并说明理由; 上是否存在点
上是否存在点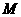 ,使
,使 ∽
∽ ?若存在,求出点
?若存在,求出点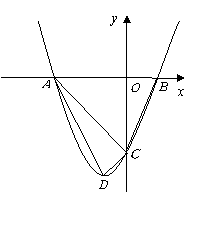

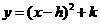 的顶点坐标为D(-1,-4),
的顶点坐标为D(-1,-4),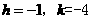 . ……………………………………………………………………2分
. ……………………………………………………………………2分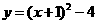 .
.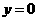 时,
时,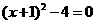 .
解之,得
.
解之,得 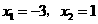 .
.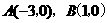 .
. 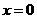 时,
时,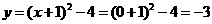 ,
,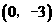 .……………………………………………………………………4分
.……………………………………………………………………4分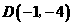 ,作抛物线的对称轴
,作抛物线的对称轴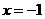 交
交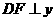 轴于点
轴于点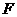 .易知
.易知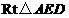 中,
中,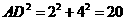 ;
;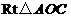 中,
中,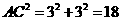 ;
; 中,
中,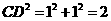 ;
;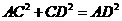 .
. 为等腰直角三角形,
为等腰直角三角形,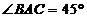 ,
,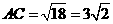 .
.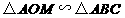 ,得
,得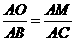 .
.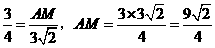 . ……………………………………………………8分
. ……………………………………………………8分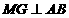 于点
于点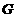 ,则
,则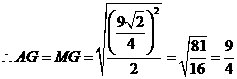 ,
,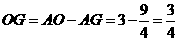 .
.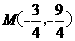 . …………………………………………………10分
. …………………………………………………10分

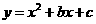 的顶点为
的顶点为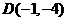 ,与
,与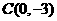 ,与
,与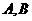 两点(点A在点B的左边).
两点(点A在点B的左边).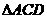 为直角三角形;
为直角三角形;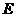 在抛物线的对称轴上,抛物线上是否存在点F,使以A,B,E,F四点为顶点的四边形为平行四边形?若存在,求出满足条件的点F的坐标;若不存在,请说明理由.
在抛物线的对称轴上,抛物线上是否存在点F,使以A,B,E,F四点为顶点的四边形为平行四边形?若存在,求出满足条件的点F的坐标;若不存在,请说明理由.
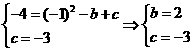 ,所以抛物线的解析式为
,所以抛物线的解析式为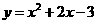 ;
;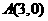 ,
,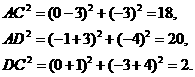
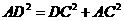 ,所以
,所以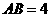 ,假设存在这样的点F,设
,假设存在这样的点F,设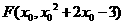 ,所以
,所以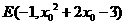 ,
,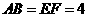 ,即
,即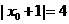 ,所以
,所以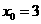 或
或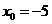 ,因此点F的坐标为
,因此点F的坐标为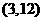 或
或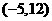 。
。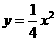 交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2<0).
交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2<0).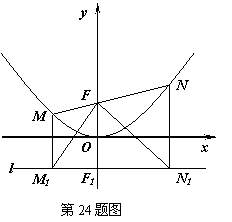

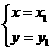 和
和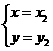 是方程组
是方程组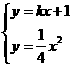 的两组解,解方程组消元得
的两组解,解方程组消元得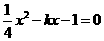 ,依据“根与系数关系”得
,依据“根与系数关系”得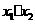 =-4
=-4
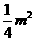 ,计算知NN1=
,计算知NN1=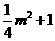 , NF=
, NF=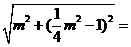
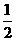 (MM1+NN1)=
(MM1+NN1)=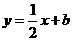 交折现OAB与点E。
交折现OAB与点E。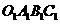 ,试探究四边形
,试探究四边形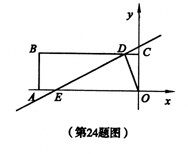
 ;
;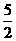 ;
;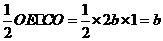
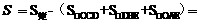
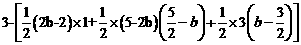
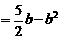
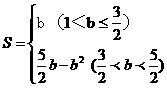
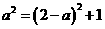 ,∴
,∴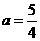 ∴
∴