摘要:10.如图.等边△ABC中.AO是∠BAC的角平分线.D为AO上一点.以CD为一边且在CD下方作等边△CDE,连结BE. (1) 求证:△ACD≌△BCE, (2) 延长BE至Q, P为BQ上一点.连结CP.CQ使CP=CQ=5, 若BC=8时.求PQ的长. [答案]:(1)证明ABC和△CDE均为等边三角形. ∴AC=BC , CD=CE 且∠ACB=∠DCE=60° ∵∠ACD+∠DCB=∠DCB+∠BCE=60° ∴∠ACD=∠BCE ∴△ACD≌△BCE (2)解:作CH⊥BQ交BQ于H, 则PQ=2HQ 在Rt△BHC中 .由已知和(1)得∠CBH=∠CAO=30°.∴ CH=4 在Rt△CHQ中.HQ= ∴PQ=2HQ=6
网址:http://m.1010jiajiao.com/timu3_id_496626[举报]
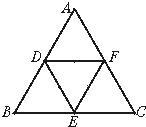 9、如图,等边△ABC中,D、E、F分别是AB、BC、CA边上的中点,那么图中有
9、如图,等边△ABC中,D、E、F分别是AB、BC、CA边上的中点,那么图中有 5、如图,等边△ABC中,BD=CE,AD与BE交于P,AQ⊥BE,垂足为Q,PD=2,PQ=6,则BE的长为( )
5、如图,等边△ABC中,BD=CE,AD与BE交于P,AQ⊥BE,垂足为Q,PD=2,PQ=6,则BE的长为( )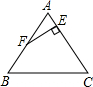 如图,等边△ABC中,F是AB中点,EF⊥AC于E,若△ABC的边长为10,则AE=
如图,等边△ABC中,F是AB中点,EF⊥AC于E,若△ABC的边长为10,则AE=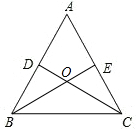 如图,等边△ABC中,点D、E分别是边AB、AC的中点,CD、BE交于点O,求∠BOC是多少度?
如图,等边△ABC中,点D、E分别是边AB、AC的中点,CD、BE交于点O,求∠BOC是多少度?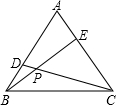 如图,等边△ABC中,D、E分别在AB、AC上,且AD=CE,BE、CD交于点P,若∠ABE:∠CBE=1:2,则∠BDP=
如图,等边△ABC中,D、E分别在AB、AC上,且AD=CE,BE、CD交于点P,若∠ABE:∠CBE=1:2,则∠BDP=