1. (2011江苏南京,28,11分)
问题情境
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的长为x,周长为y,则y与x的函数关系式为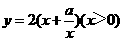 .
.
探索研究
⑴我们可以借鉴以前研究函数的经验,先探索函数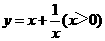 的图象性质.
的图象性质.
① 填写下表,画出函数的图象:
|
x |
…… |
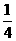 |
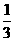 |
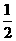 |
1 |
2 |
3 |
4 |
…… |
|
y |
…… |
|
|
|
|
|
|
|
…… |
②观察图象,写出该函数两条不同类型的性质;
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数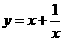 (x>0)的最小值.
(x>0)的最小值.
解决问题
⑵用上述方法解决“问题情境”中的问题,直接写出答案.
[答案]解:⑴①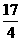 ,
,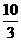 ,
,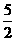 ,2,
,2,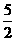 ,
,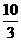 ,
,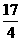 .
.
函数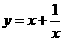
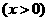 的图象如图.
的图象如图.
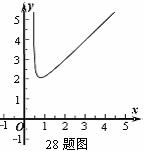
②本题答案不唯一,下列解法供参考.
当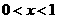 时,
时,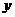 随
随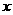 增大而减小;当
增大而减小;当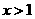 时,
时,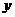 随
随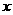 增大而增大;当
增大而增大;当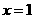 时函数
时函数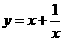
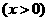 的最小值为2.
的最小值为2.
③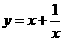
=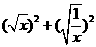
=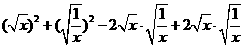
=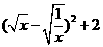
当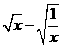 =0,即
=0,即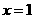 时,函数
时,函数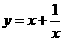
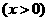 的最小值为2.
的最小值为2.
⑵当该矩形的长为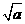 时,它的周长最小,最小值为
时,它的周长最小,最小值为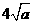 .
.
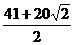 π?
π?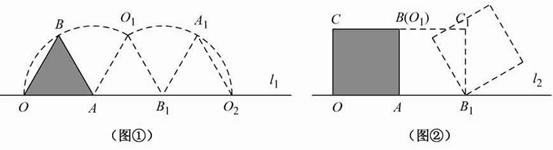
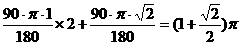 .
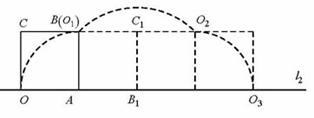
.
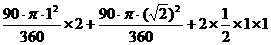 =1+π.
=1+π.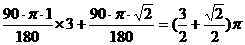 .
.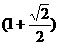 π+
π+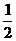 π.
π. (
(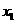 ,0)、
,0)、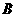 (
( ,0)两点,且
,0)两点,且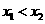 ,与
,与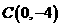 ,其中
,其中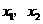 是方程
是方程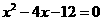 的两个根。
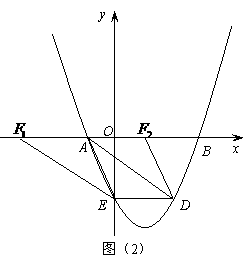
的两个根。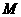 是线段
是线段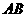 上的一个动点,过点
上的一个动点,过点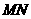 ∥
∥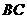 ,交
,交 于点
于点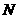 ,连接
,连接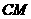 ,当
,当 的面积最大时,求点
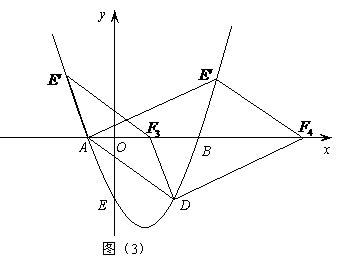
的面积最大时,求点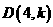 在(1)中抛物线上,点
在(1)中抛物线上,点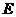 为抛物线上一动点,在
为抛物线上一动点,在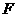 ,使以
,使以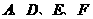 为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点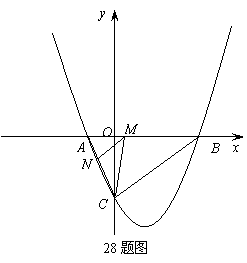

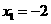 ,
,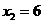 。
。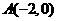 ,
,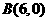 。
。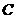 ,故设抛物线的解析式为
,故设抛物线的解析式为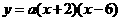 ,将点
,将点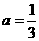 。
。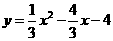 。
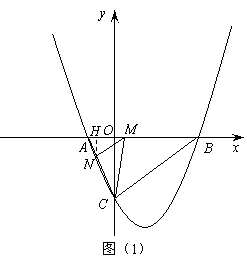
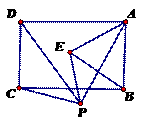
。 ,0),过点
,0),过点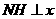 轴于点
轴于点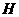 (如图(1))。
(如图(1))。 ,0),点
,0),点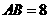 ,
,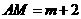 。
。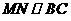 ,∴
,∴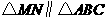 。
。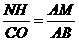 ,∴
,∴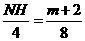 ,∴
,∴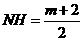 。
。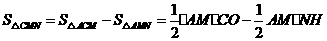

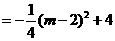 。
。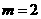 时,
时, 有最大值4。
有最大值4。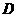 (4,
(4,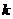 )在抛物线
)在抛物线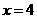 时,
时,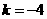 ,
,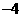 )。
)。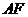 为平行四边形的边时,
为平行四边形的边时,

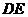 ,
,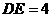 。
。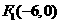 ,
,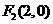 。
。 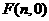 ,
,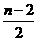 ,0)。
,0)。 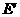 的坐标为(
的坐标为(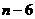 ,4)。
,4)。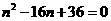 。
。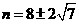 。
。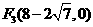 ,
,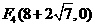 。
。
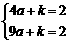 ,解得a=0,这与条件a>0不符,
,解得a=0,这与条件a>0不符,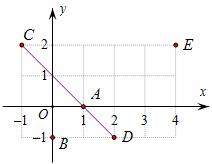
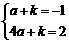 ,解得
,解得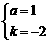
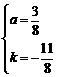 .
.
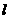 上,如图⑴,AB=6cm,BC=8cm,
上,如图⑴,AB=6cm,BC=8cm, ,求四边形DHCF的面积.
,求四边形DHCF的面积.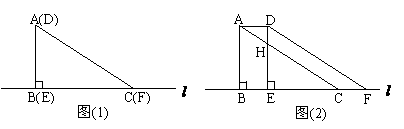

 .
.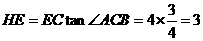 .
.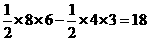 cm2.
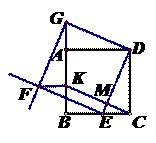
cm2.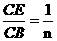 时,请直接写出
时,请直接写出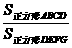 的值.
的值.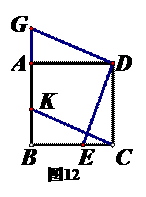
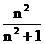
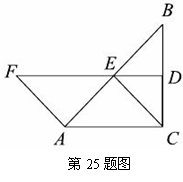

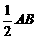 ,∵DE垂直平分BC,∴ BE=CE
,∵DE垂直平分BC,∴ BE=CE