摘要： 如图6.点D.E在△ABC的边BC上.连接AD.AE. ①AB＝AC,②AD＝AE,③BD＝CE.以此三个等式中的两个作为命题的题设.另一个作为命题的结论.构成三个命题:①②③,①③②,②③①. (1)以上三个命题是真命题的为 , (2)请选择一个真命题进行证明(先写出所选命题.然后证明). [答案](1)①②③,①③②,②③①.················································· 3分 6分
网址：http://m.1010jiajiao.com/timu3_id_496630[举报]
（1）如图1，请你类比直线和一个圆的三种位置关系，在图1的①、②、③中，分别各画出一条直线，使它与两个圆都相离、与两个圆都相切、与一个圆相离且与另一个圆相交，并在图1的④中也画上一条直线，使它与两个圆具有不同于前面3种情况的位置关系；
（2）如图2，点A、B在直线MN上，AB=11厘米，⊙A、⊙B的半径均为1厘米．⊙A以每秒2厘米的速度自左向右运动，与此同时，⊙B的半径也不断增大，其半径r（厘米）与时间t（秒）之间的关系式为r=1+t（t≥0）．请直接写出点A出发后多少秒两圆内切？
查看习题详情和答案>>
（2）如图2，点A、B在直线MN上，AB=11厘米，⊙A、⊙B的半径均为1厘米．⊙A以每秒2厘米的速度自左向右运动，与此同时，⊙B的半径也不断增大，其半径r（厘米）与时间t（秒）之间的关系式为r=1+t（t≥0）．请直接写出点A出发后多少秒两圆内切？
查看习题详情和答案>>
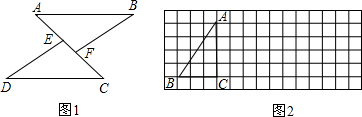
（2012•福州）（1）如图1，点E、F在AC上，AB∥CD，AB=CD，AE=CF，求证：△ABF≌△CDE
（2）如图2，方格纸中的每个小方格是边长为1个单位长度的正方形．
①画出将Rt△ABC向右平移5个单位长度后的Rt△A1B1C1
②再将Rt△A1B1C1绕点C1顺时针旋转90°，画出旋转后的Rt△A2B2C2，并求出旋转过程中线段A1C1所扫过的面积（结果保留π）
查看习题详情和答案>>
（2）如图2，方格纸中的每个小方格是边长为1个单位长度的正方形．
①画出将Rt△ABC向右平移5个单位长度后的Rt△A1B1C1
②再将Rt△A1B1C1绕点C1顺时针旋转90°，画出旋转后的Rt△A2B2C2，并求出旋转过程中线段A1C1所扫过的面积（结果保留π）
如图1，在正方形ABCD中，点E、F分别为边BC、CD的中点，AF、DE相交于点G，则可得结论：①AF=DE，②AF⊥DE（不须证明）．
（1）如图②，若点E、F不是正方形ABCD的边BC、CD的中点，但满足CE=DF，则上面的结论①、②是否仍然成立；（请直接回答“成立”或“不成立”）
（2）如图③，若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上，且CE=DF，此时上面的结论①、②是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由．
（3）如图④，在（2）的基础上，连接AE和EF，若点M、N、P、Q分别为AE、EF、FD、AD的中点，请先判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种，并写出证明过程．
查看习题详情和答案>>
（1）如图②，若点E、F不是正方形ABCD的边BC、CD的中点，但满足CE=DF，则上面的结论①、②是否仍然成立；（请直接回答“成立”或“不成立”）
（2）如图③，若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上，且CE=DF，此时上面的结论①、②是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由．
（3）如图④，在（2）的基础上，连接AE和EF，若点M、N、P、Q分别为AE、EF、FD、AD的中点，请先判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种，并写出证明过程．
查看习题详情和答案>>
问题情境：如图1，在直角三角形ABC中，∠BAC=90°，AD⊥BC于点D，可知：∠BAD=∠C（不需要证明）；
特例探究：如图2，∠MAN=90°，射线AE在这个角的内部，点B、C在∠MAN的边AM、AN上，且AB=AC，CF⊥AE于点F，BD⊥AE于点D．证明：△ABD≌△CAF；
归纳证明：如图3，点B，C在∠MAN的边AM、AN上，点E，F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC，∠1=∠2=∠BAC．求证：△ABE≌△CAF；
拓展应用：如图4，在△ABC中，AB=AC，AB＞BC．点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC．若△ABC的面积为15，则△ACF与△BDE的面积之和为
查看习题详情和答案>>
特例探究：如图2，∠MAN=90°，射线AE在这个角的内部，点B、C在∠MAN的边AM、AN上，且AB=AC，CF⊥AE于点F，BD⊥AE于点D．证明：△ABD≌△CAF；
归纳证明：如图3，点B，C在∠MAN的边AM、AN上，点E，F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC，∠1=∠2=∠BAC．求证：△ABE≌△CAF；
拓展应用：如图4，在△ABC中，AB=AC，AB＞BC．点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC．若△ABC的面积为15，则△ACF与△BDE的面积之和为
5
5
．
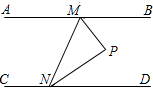（2013•晋江市质检）如图，动点M、N分别在直线AB与CD上，且AB∥CD，∠BMN与∠MND的角平分线相交于点P，若以MN为直径作⊙O，则点P与⊙O的位置关系是（ ）