0 49398 49406 49412 49416 49422 49424 49428 49434 49436 49442 49448 49452 49454 49458 49464 49466 49472 49476 49478 49482 49484 49488 49490 49492 49493 49494 49496 49497 49498 49500 49502 49506 49508 49512 49514 49518 49524 49526 49532 49536 49538 49542 49548 49554 49556 49562 49566 49568 49574 49578 49584 49592 447348
 按图1的方法把圆锥的侧面展开,得到图2,其半径OA=3,圆心角∠AOB=120°,则AB的长为(■).
按图1的方法把圆锥的侧面展开,得到图2,其半径OA=3,圆心角∠AOB=120°,则AB的长为(■).
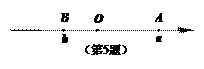 如图,数轴上A,B两点分别对应实数a,b,则下列结论正确的是( ■).
如图,数轴上A,B两点分别对应实数a,b,则下列结论正确的是( ■).

