0 49630 49638 49644 49648 49654 49656 49660 49666 49668 49674 49680 49684 49686 49690 49696 49698 49704 49708 49710 49714 49716 49720 49722 49724 49725 49726 49728 49729 49730 49732 49734 49738 49740 49744 49746 49750 49756 49758 49764 49768 49770 49774 49780 49786 49788 49794 49798 49800 49806 49810 49816 49824 447348
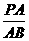 =
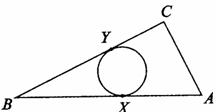
=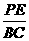 .∵AC=1,BC=2,∴AB=
.∵AC=1,BC=2,∴AB= 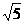 .设PC=x,则PA=AC-PC=1-x,PC=PE,
.设PC=x,则PA=AC-PC=1-x,PC=PE,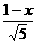 =
=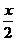 ,∴x=
,∴x=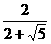 .(6分)
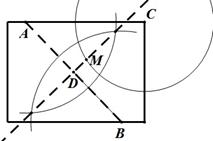
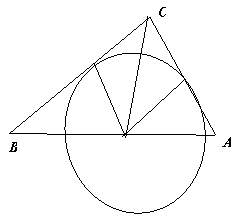
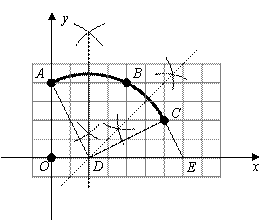
② 如图3,同理可得:当⊙P与Rt△ABC的边AB和AC相切时,
.(6分)
② 如图3,同理可得:当⊙P与Rt△ABC的边AB和AC相切时,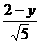 =
=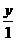 ,∴y=
,∴y= 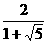 (7分)
③ 如图4,同理可得:当⊙P与Rt△ABC的边BC和AC相切时,设PF=z,则
(7分)
③ 如图4,同理可得:当⊙P与Rt△ABC的边BC和AC相切时,设PF=z,则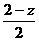 =
=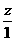 ,∴z=
,∴z=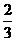 (8分)由①,②,③可知:∵
(8分)由①,②,③可知:∵ 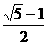 ,
,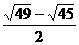 >0,∴y>x.
>0,∴y>x. 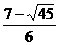 >0,∴2
>0,∴2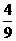 π.(10分)
π.(10分)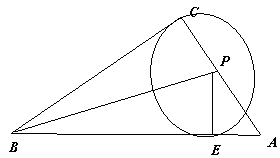
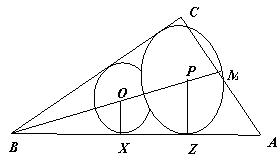

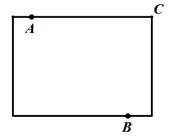
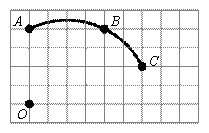
 (第23题答图1)
(第23题答图1)
(第23题答图1)
(第23题答图1) 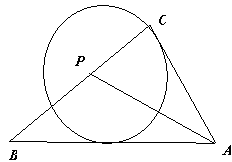
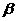 .
.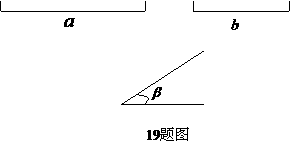 已知:
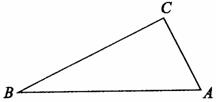
已知: 求作:△ABC使边BC=a,AC= b,∠C=
求作:△ABC使边BC=a,AC= b,∠C=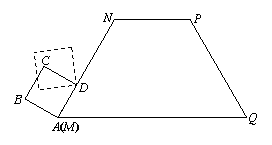

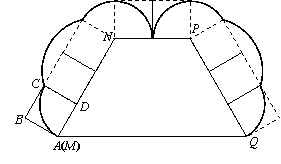

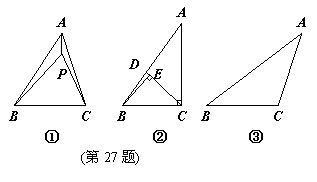

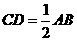 ,∴CD=BD.
,∴CD=BD.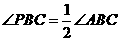 ,
,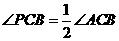 .
.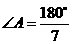 .∴该三角形三个内角的度数分别为
.∴该三角形三个内角的度数分别为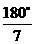 、
、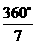 、
、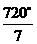 .
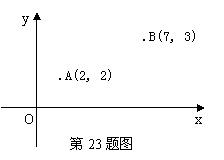
. 解:已知:
解:已知:
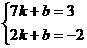 解得:
解得: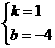 ·
·


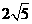
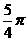
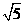 ,DE=5
,DE=5