0 49689 49697 49703 49707 49713 49715 49719 49725 49727 49733 49739 49743 49745 49749 49755 49757 49763 49767 49769 49773 49775 49779 49781 49783 49784 49785 49787 49788 49789 49791 49793 49797 49799 49803 49805 49809 49815 49817 49823 49827 49829 49833 49839 49845 49847 49853 49857 49859 49865 49869 49875 49883 447348
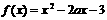 在区间[1,2]上存在反函数的充分必要条件是 ( )
在区间[1,2]上存在反函数的充分必要条件是 ( )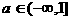 B.
B.
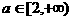
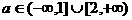 D.
D.
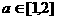
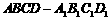 中,P是侧面
中,P是侧面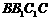 内一动点,若P到直线BC与
内一动点,若P到直线BC与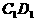 的距离相等,则动点P的轨迹所在的曲线是 ( )
的距离相等,则动点P的轨迹所在的曲线是 ( )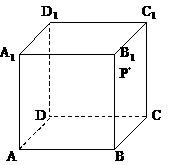
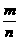 等于 ( )
等于 ( )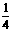 C.
C.
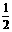 D.
D.
 ,且
,且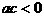 ,那么下列选项中一定成立的是 ( )
,那么下列选项中一定成立的是 ( )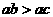 B.
B. 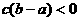 C.
C.
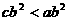 D.
D.
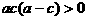
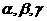 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: ,
,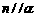 ,则
,则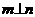 ②若
②若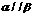 ,
,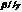 ,
, ,则
,则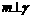
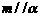 ,
,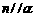 ,则
,则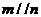 ④若
④若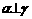 ,
,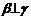 ,则
,则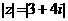 的复数
的复数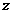 在复平面上对应点的轨迹是 ( )
在复平面上对应点的轨迹是 ( )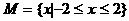 ,
,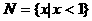 ,则
,则 等于 ( )
等于 ( ) B.
B.
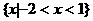 C.
C. 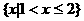 D.
D.
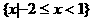
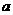 、b、c,且
、b、c,且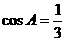 .
.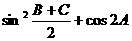 的值;
的值;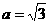 ,求bc的最大值.
,求bc的最大值.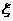 .
. .
.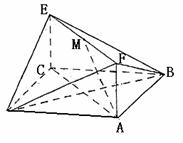 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, AB=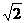 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.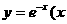 ≥0)在点M(t,e--t)处的切线
≥0)在点M(t,e--t)处的切线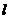 与x轴y轴所围成的三角形面积为S(t).
与x轴y轴所围成的三角形面积为S(t).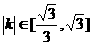 ,求实数m的取值范围;
,求实数m的取值范围;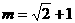 时,ΔAPQ的内心恰好是点M,求此双曲线的方程.
时,ΔAPQ的内心恰好是点M,求此双曲线的方程.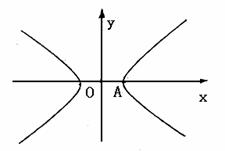
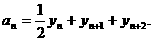
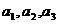 及
及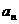 ;
;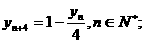
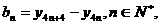 证明
证明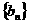 是等比数列.
是等比数列.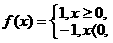 则不等式
则不等式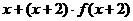 ≤5的解集是
.
≤5的解集是
.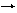

 (14)已知平面上三点A、B、C满足
(14)已知平面上三点A、B、C满足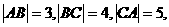 则AB· BC+BC·CA+CA·AB的值等于 .
则AB· BC+BC·CA+CA·AB的值等于 .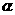 和平面
和平面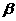 交于直线
交于直线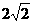 ,相应于焦点F(c,0)(
,相应于焦点F(c,0)(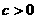 )的准线
)的准线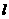 与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.
与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.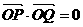 ,求直线PQ的方程;
,求直线PQ的方程;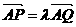 (
(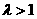 ),过点P且平行于准线
),过点P且平行于准线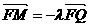 .
.