摘要: 如图①.P为△ABC内一点.连接PA.PB.PC.在△PAB.△PBC和△PAC中.如果存在一个三角形与△ABC相似.那么就称P为△ABC的自相似点. ⑴如图②.已知Rt△ABC中.∠ACB=90°.∠ACB>∠A.CD是AB上的中线.过点B作BE⊥CD.垂足为E.试说明E是△ABC的自相似点. ⑵在△ABC中.∠A<∠B<∠C. ①如图③.利用尺规作出△ABC的自相似点P(写出作法并保留作图痕迹), ②若△ABC的内心P是该三角形的自相似点.求该三角形三个内角的度数. [答案]解:⑴在Rt △ABC中.∠ ACB=90°.CD是AB上的中线.∴.∴CD=BD. ∴∠BCE=∠ABC.∵BE⊥CD.∴∠BEC=90°.∴∠BEC=∠ACB.∴△BCE∽△ABC. ∴E是△ABC的自相似点. ⑵①作图略. 作法如下:(i)在∠ABC内.作∠CBD=∠A, (ii)在∠ACB内.作∠BCE=∠ABC,BD交CE于点P. 则P为△ABC的自相似点. ②连接PB.PC.∵P为△ABC的内心.∴.. ∵P为△ABC的自相似点.∴△BCP∽△ABC. ∴∠PBC=∠A.∠BCP=∠ABC=2∠PBC =2∠A. ∠ACB=2∠BCP=4∠A.∵∠A+∠ABC+∠ACB=180°. ∴∠A+2∠A+4∠A=180°. ∴.∴该三角形三个内角的度数分别为...
网址:http://m.1010jiajiao.com/timu3_id_497275[举报]
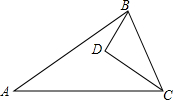 如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=8,BC=5,则BD的长为
如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=8,BC=5,则BD的长为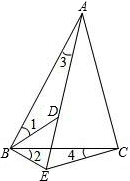 如图,D为△ABC内一点,E为△ABC外一点,且∠1=∠2,∠3=∠4,找出图中的两对相似三角形并说明理由.
如图,D为△ABC内一点,E为△ABC外一点,且∠1=∠2,∠3=∠4,找出图中的两对相似三角形并说明理由. 一个三角形与△ABC相似,那么就称P为△ABC的自相似点.已知△ABC中,∠A<∠B<∠C.
一个三角形与△ABC相似,那么就称P为△ABC的自相似点.已知△ABC中,∠A<∠B<∠C. 如图,D为△ABC内任意一点,求证:∠BDC>∠A
如图,D为△ABC内任意一点,求证:∠BDC>∠A 如图,O为△ABC内任意一点,OD⊥AB,OE⊥AC,OF⊥BC,若OD=OE=OF,连接OA,OB,OC,下列说法不一定正确的是( )
如图,O为△ABC内任意一点,OD⊥AB,OE⊥AC,OF⊥BC,若OD=OE=OF,连接OA,OB,OC,下列说法不一定正确的是( )