摘要： 如图.抛物线y=ax2+bx(a0)与双曲线y= 相交于点A.B. 已知点B的坐标为.点A在第一象限内.且tan∠AOx=4. 过点A作直线AC∥x轴.交抛物线于另一点C． (1)求双曲线和抛物线的解析式, (2)计算△ABC的面积, (3)在抛物线上是否存在点D.使△ABD的面积等于△ABC的面积．若存在.请你写出点D的坐标,若不存在.请你说明理由． [答案](1)把点B的坐标.代入y=. 得:-2=.∴k=4． 即双曲线的解析式为:y= ． 设A点的坐标为(m.n).∵A点在双曲线上.∴mn=4．-① 又∵tan∠AOx=4.∴=4. 即m=4n．-② 又①.②.得:n2=1,∴n=±1. ∵A点在第一象限.∴n=1,m=4 . ∴A点的坐标为(1.4) 把A.B点的坐标代入y=ax2+b x.得:解得a=1.b=3, ∴抛物线的解析式为:y=x2+3x ,(2)∵AC∥x轴.∴点C的纵坐标y=4. 代入y=x2+3x.得方程x2+3x-4=0.解得x1=-4.x2=1． ∴C点的坐标为.且AC=5. 又△ABC的高为6.∴△ABC的面积=×5×6=15 , (3)存在D点使△ABD的面积等于△ABC的面积. 过点C作CD∥AB交抛物线于另一点D ． 因为直线AB相应的一次函数是:y=2x+2.且C点的坐标为.CD∥AB. 所以直线CD相应的一次函数是:y=2x+12. 解方程组 得所以点D的坐标是
网址：http://m.1010jiajiao.com/timu3_id_496462[举报]
如图，抛物线y=ax2+bx-3与x轴交于两点A（1，0）、B（3，0），与y轴交于点D．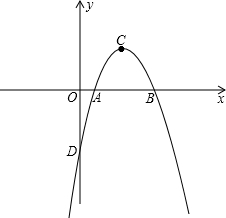
（1）求抛物线的解析式；
（2）在抛物线是否存在一点P，使得△BDP是以BD为斜边的直角三角形，若存在，请求出点P的坐标；若不存在，请说明理由；
（3）在x轴下方的抛物线上是否存在点M，过M作MN⊥x轴于点N，使以A、M、N为顶点的三角形与△BCD相似？若存在，则求出点M的坐标；若不存在，请说明理由． 查看习题详情和答案>>
（1）求抛物线的解析式；
（2）在抛物线是否存在一点P，使得△BDP是以BD为斜边的直角三角形，若存在，请求出点P的坐标；若不存在，请说明理由；
（3）在x轴下方的抛物线上是否存在点M，过M作MN⊥x轴于点N，使以A、M、N为顶点的三角形与△BCD相似？若存在，则求出点M的坐标；若不存在，请说明理由． 查看习题详情和答案>>
如图，抛物线y=ax2-4ax+c交x轴于A、B两点，交y轴于C点，点D（4，-3）在抛物
线上，且四边形ABDC的面积为18．
（1）求抛物线的函数关系式；
（2）若正比例函数y=kx的图象将四边形ABDC的面积分为1：2的两部分，求k的值；
（3）将△AOC沿x轴翻折得到△AOC′，问：是否存在这样的点P，以P为位似中心，将△AOC′放大为原来的两倍后得到△EPG（即△EPG∽△AOC′，且相似比为2），使得点E、G恰好在抛物线上？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由． 查看习题详情和答案>>
线上，且四边形ABDC的面积为18．（1）求抛物线的函数关系式；
（2）若正比例函数y=kx的图象将四边形ABDC的面积分为1：2的两部分，求k的值；
（3）将△AOC沿x轴翻折得到△AOC′，问：是否存在这样的点P，以P为位似中心，将△AOC′放大为原来的两倍后得到△EPG（即△EPG∽△AOC′，且相似比为2），使得点E、G恰好在抛物线上？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由． 查看习题详情和答案>>
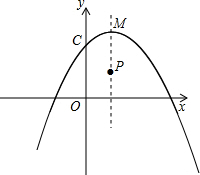如图，抛物线y=ax2+bx+c的顶点M的坐标是（1，3），且与y轴相交于点C（0，2），P（1，1）是抛物线对称轴上的一点．请回答下列问题：（1）写出抛物线的解析式
（2）点Q是抛物线上的一点，且使△CPQ的面积等于△CMP的面积，则所有满足条件的点Q的个数为：
R是小圆半径r的4倍．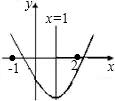
如图，抛物线y=ax2+bx+c的对称轴是x=1，下列结论：①b＜0；②（a+c）2＞b2；③2a+b-c＞0；④3b＜2c．其中正确的结论有