摘要： (2011江苏连云港.25.10分)如图.抛物线与x轴交于A.B两点.与y轴交于点C.其顶点在直线y=-2x上. (1)求a的值, (2)求A,B两点的坐标; (3)以AC,CB为一组邻边作□ABCD,则点D关于x轴的对称点D´是否在该抛物线上?请说明理由. [答案]解:(1)∵二抛物线的顶点坐标为.∴x=1,∵顶点在直线y=-2x上.所以y=-2,即顶点坐标为.∴-2=-1+a,即a=-4;(2)二次函数的关系式为.当y=0时. .解之得:.即A如图所示:直线BD//AC,AD//BC,因为A,C(0,),所以直线AB的解析式为,所以设BD的解析式为,因为B(3,0),所以b=,直线BD的解析式为:,同理可得:直线AD的解析式为:,因此直线BD与CD的交点坐标为:(2,),则点D关于x轴的对称点D´是(2,-),当x=2时代入得,y=,所以D´在二次函数的图象上.
网址：http://m.1010jiajiao.com/timu3_id_496470[举报]
（2013•绍兴模拟）如图，抛物线与x轴交于A，B两点，点B坐标为（3，0）顶点P的坐标为（1，-4），以AB为直径作圆，圆心为D，过P向右侧作⊙D的切线，切点为C．（1）求抛物线的解析式；
（2）请通过计算判断抛物线是否经过点C；
（3）设M，N 分别为x轴，y轴上的两个动点，当四边形PNMC的周长最小时，请直接写出M，N两点的坐标．
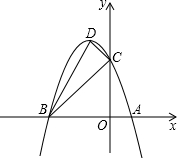（2013•营口）如图，抛物线与x轴交于A（1，0）、B（-3，0）两点，与y轴交于点C（0，3），设抛物线的顶点为D．（1）求该抛物线的解析式与顶点D的坐标．
（2）试判断△BCD的形状，并说明理由．
（3）探究坐标轴上是否存在点P，使得以P、A、C为顶点的三角形与△BCD相似？若存在，请直接写出点P的坐标；若不存在，请说明理由．
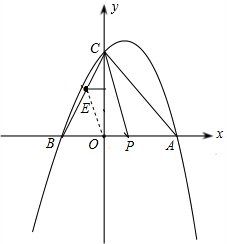如图，抛物线与x轴交于A（x1，0），B（x2，0）两点，且x1＞x2，与y轴交于点C（0，4），其中x1，x2是方程x2-2x-8=0的两个根．（1）求这条抛物线的解析式；
（2）点P是线段AB上的动点，过点P作PE∥AC，交BC于点E，连接CP，当△CPE的面积最大时，求点P的坐标；
（3）探究：若点Q是抛物线对称轴上的点，是否存在这样的点Q，使△QBC成为等腰三角形？若存在，请直接写出所有符合条件的点Q的坐标；若不存在，请说明理由． 查看习题详情和答案>>
（2012•历下区一模）如图，抛物线与x轴交于A（-1，0），B（4，0）两点，与y轴交于C（0，3），M是抛物线对称轴上的任意一点，则△AMC的周长最小值是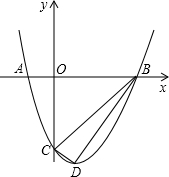
线的顶点为D．