摘要： 在平面直角坐标系中.如图1.将n个边长为1的正方形并排组成矩形OABC.相邻两边OA和OC分别落在x轴和y轴的正半轴上.设抛物线y=ax2+bx+c(a<0)过矩形顶点B.C. (1)当n＝1时.如果a=-1.试求b的值, (2)当n＝2时.如图2.在矩形OABC上方作一边长为1的正方形EFMN.使EF在线段CB上.如果M.N两点也在抛物线上.求出此时抛物线的解析式, (3)将矩形OABC绕点O顺时针旋转.使得点B落到x轴的正半轴上.如果该抛物线同时经过原点O. ①试求出当n=3时a的值, ②直接写出a关于n的关系式. [解](1)由题意可知.抛物线对称轴为直线x=. ∴-=.得b=1, (2)设所求抛物线的解析式为y=ax2+bx+1. 由对称性可知抛物线经过点B(2.1)和点M(.2). ∴解得 ∴所求抛物线解析式为y=-x2+ x+1, (3)①当n=3时.OC=1.BC=3. 设所求抛物线的解析式为y=ax2+bx. 过C作CD⊥OB于点D.则Rt△OCD∽Rt△CBD. ∴==. 设OD=t.则CD=3t. ∵OD2+CD2=OC2. ∴(3t)2+ t 2=12.∴ t==. ∴C(.).又B(.0). ∴把B.C坐标代入抛物线解析式.得 解得:a=-, ②a=-.
网址：http://m.1010jiajiao.com/timu3_id_496465[举报]
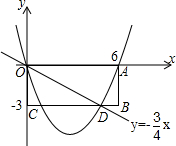
矩形OABC在平面直角坐标系中位置如图所示，A、C两点的坐标分别为A（6，0），C（0，-3），直线y=-
x与BC边
相交于D点．
（1）求点D的坐标；
（2）若抛物线y=ax2-
x经过点A，求此抛物线的表达式及对称轴；
（3）设（2）中的抛物线的对称轴与直线OD交于点M，点P为坐标轴上一动点，以P、O、M为顶点的三角形与△OCD相似，求出点M的坐标和符合条件的点P的坐标；
（4）当（3）中符合条件的△POM面积最大时，过点O的直线l将其面积分为1：3两部分，请直接写出直线l的解析式．
查看习题详情和答案>>
| 3 |
| 4 |
相交于D点．（1）求点D的坐标；
（2）若抛物线y=ax2-
| 9 |
| 4 |
（3）设（2）中的抛物线的对称轴与直线OD交于点M，点P为坐标轴上一动点，以P、O、M为顶点的三角形与△OCD相似，求出点M的坐标和符合条件的点P的坐标；
（4）当（3）中符合条件的△POM面积最大时，过点O的直线l将其面积分为1：3两部分，请直接写出直线l的解析式．
（2013•襄城区模拟）矩形OABC在平面直角坐标系中位置如图所示，A、c两点的坐标分别为A（6，0），C（0，3），直线y=-| 3 |
| 4 |
（1）若抛物线y=ax2-
| 9 |
| 4 |
（2）在（1）中的抛物线的对称轴上取一点E，求出EA+ED的最小值；
（3）设（1）中的抛物线的对称轴与直线OD交于点M，点P为对称轴上一动点，以P，O，M为顶点的三角形与△OCD相似，求符合条件的点P的坐标．
在平面直角坐标系中，如图，已知△ABC三个顶点的坐标分别为A（1，-4），B（5，-4），C（4，-1），
△ABC三个顶点A，B，C在平面直角坐标系中位置如图所示．将△ABC绕C点顺时针旋转90°，画出旋转后的△A2B2C2，并写出A2的坐标．
（2013•邵东县模拟）在平面直角坐标系中，如图所示，△AOB是边长为2的等边三角形，将△AOB绕着点B按顺时针方向旋转得到△DCB，使得点D落在x轴的正半轴上，连接OC，AD．