摘要: 孔明是一个喜欢探究钻研的同学.他在和同学们一起研究某条抛物线的性质时.将一把直角三角板的直角顶点置于平面直角坐标系的原点O.两直角边与该抛物线交于A.B两点.请解答以下问题: (1)若测得.求的值, (2)对同一条抛物线.孔明将三角板绕点O旋转到如图2所示位置时.过B作BF⊥x轴于点F.测得OF=1.写出此时点B的坐标.并求点A的横坐标, (3)对该抛物线.孔明将三角板绕点O旋转任意角度时惊奇地发现.交点A.B的连线段总经过一个固定的点.试说明理由并求出该点的坐标. [答案]解:(1)设线段AB与y轴的交点为C.由抛物线的对称性可得C为AB中点. ∵ .∠AOB=90°. ∴AC=OC=BC=2.∴B. 将B代入抛物线得.. (2)解法一:过点A作AE⊥x轴于点E. ∵点B的横坐标为1.∴B (1.). ∴. 又∵∠AOB=90°.易知∠AOE=∠OBF.又∠AEO=∠OFB=90°. ∴△AEO∽△OFB.∴ ∴AE=2OE. 设点A(.).则OE=m..∴ ∴m=4.即点A的横坐标为-4. 解法二:过点A作AE⊥x轴于点E. ∵点B的横坐标为1.∴B (1.). ∴ ∵∠AOB=90°.易知∠AOE=∠OBF. ∴.∴AE=2OE. 设点A(-.)(m>0).则OE=m..∴ ∴m=4.即点A的横坐标为-4. 解法三:过点A作AE⊥x轴于点E. ∵点B的横坐标为1.∴B (1.). 设A(-.)(m>0).则 ... ∵∠AOB=90°.∴. ∴. 解得:m=4.即点A的横坐标为-4. (3)解法一:设A(.)(m>0).B(.)(n>0). 设直线AB的解析式为:y=kx+b. 则. ×m得.. ∴ 又易知△AEO∽△OFB.∴.∴.∴mn=4. ∴.由此可知不论k为何值.直线AB恒过点. (说明:写出定点C的坐标就给2分) 解法二:设A(.).B(.). 直线AB与y轴的交点为C.根据.可得 . 化简.得. 又易知△AEO∽△OFB.∴.∴.∴mn=4.∴OC=2为固定值.故直线AB恒过其与y轴的交点C 说明:mn的值也可以通过以下方法求得. 由前可知.... 由.得:. 化简.得mn=4.
网址:http://m.1010jiajiao.com/timu3_id_496469[举报]
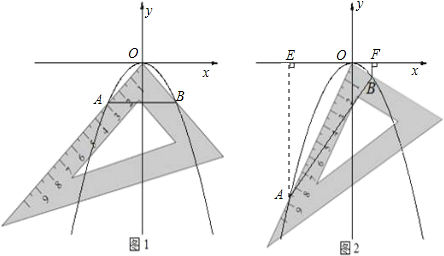
孔明是一个喜欢探究钻研的同学,他在和同学们一起研究某条抛物线y=ax2(a<0)的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点O,两直角边与该抛物线交于A、B两点,请解答以下问题:
(1)若测得OA=OB=2
(如图1),求a的值;
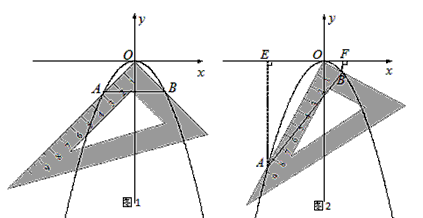
(2)对同一条抛物线,孔明将三角板绕点O旋转到如图2所示位置时,过B作BF⊥x轴于点F,测得OF=1,写出此时点B的坐标,并求点A的横坐标 ;
(3)对该抛物线,孔明将三角板绕点O旋转任意角度时惊奇地发现,交点A、B的连线段总经过一个固定的点,试说明理由并求出该点的坐标.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)若测得OA=OB=2
| 2 |
(2)对同一条抛物线,孔明将三角板绕点O旋转到如图2所示位置时,过B作BF⊥x轴于点F,测得OF=1,写出此时点B的坐标,并求点A的横坐标
(3)对该抛物线,孔明将三角板绕点O旋转任意角度时惊奇地发现,交点A、B的连线段总经过一个固定的点,试说明理由并求出该点的坐标.
 查看习题详情和答案>>
查看习题详情和答案>>
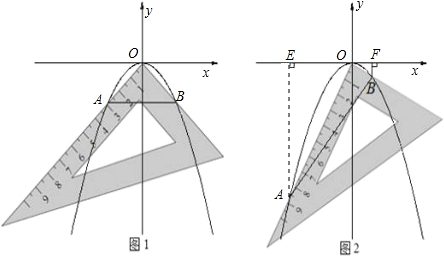
孔明是一个喜欢探究钻研的同学,他在和同学们一起研究某条抛物线y=ax2(a<0)的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点O,两直角边与该抛物线交于A、B两点,请解答以下问题:
(1)若测得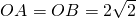 (如图1),求a的值;
(如图1),求a的值;
(2)对同一条抛物线,孔明将三角板绕点O旋转到如图2所示位置时,过B作BF⊥x轴于点F,测得OF=1,写出此时点B的坐标,并求点A的横坐标______;
(3)对该抛物线,孔明将三角板绕点O旋转任意角度时惊奇地发现,交点A、B的连线段总经过一个固定的点,试说明理由并求出该点的坐标.
查看习题详情和答案>>
孔明是一个喜欢探究钻研的同学,他在和同学们一起研究某条抛物线y=ax2(a<0)的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点O,两直角边与该抛物线交于A、B两点,请解答以下问题:
(1)若测得OA=OB=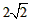 (如图1),求a的值;
(如图1),求a的值;
(2)对同一条抛物线,孔明将三角板绕点O旋转到如图2所示位置时,过B作BF⊥x轴于点F,测得OF=1,写出此时点B的坐标,并求点A的横坐标;
(3)对该抛物线,孔明将三角板绕点O旋转任意角度时惊奇地发现,交点A、B的连线段总经过一个固定的点,试说明理由并求出该点的坐标。
(1)若测得OA=OB=
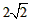 (如图1),求a的值;
(如图1),求a的值;(2)对同一条抛物线,孔明将三角板绕点O旋转到如图2所示位置时,过B作BF⊥x轴于点F,测得OF=1,写出此时点B的坐标,并求点A的横坐标;
(3)对该抛物线,孔明将三角板绕点O旋转任意角度时惊奇地发现,交点A、B的连线段总经过一个固定的点,试说明理由并求出该点的坐标。
 (如图1),求a的值;
(如图1),求a的值;
 (如图1),求a的值;
(如图1),求a的值;