0 446854 446862 446868 446872 446878 446880 446884 446890 446892 446898 446904 446908 446910 446914 446920 446922 446928 446932 446934 446938 446940 446944 446946 446948 446949 446950 446952 446953 446954 446956 446958 446962 446964 446968 446970 446974 446980 446982 446988 446992 446994 446998 447004 447010 447012 447018 447022 447024 447030 447034 447040 447048 447348
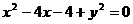 的圆心是点P,则点P到直线
的圆心是点P,则点P到直线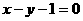 的距离是
的距离是 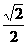 。
。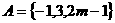 ,集合
,集合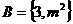 。若
。若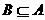 ,则实数
,则实数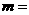
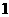 。
。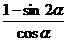 =
=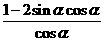 =
=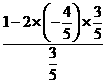 =
=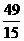 .
.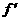 (x)>0,在(1,2)上
(x)>0,在(1,2)上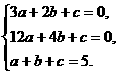 解得a=2,b=-9,c=12.
解法二:(Ⅰ)同解法一.
(Ⅱ)设
解得a=2,b=-9,c=12.
解法二:(Ⅰ)同解法一.
(Ⅱ)设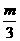 ,b=
,b=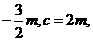
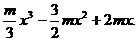 由f(l)=5, 即
由f(l)=5, 即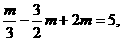 得m=6.
所以a=2,b=-9,c=12.
得m=6.
所以a=2,b=-9,c=12.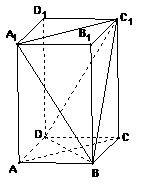 ∵ABCD是正方形 ∴BD⊥AC 又∵AC,CC1
∵ABCD是正方形 ∴BD⊥AC 又∵AC,CC1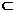 平面ACC1A1,
平面ACC1A1, ∴异面直线BC1与AC所成角的大小为
∴异面直线BC1与AC所成角的大小为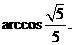
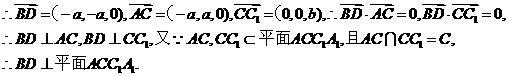
 (Ⅱ)设BD与AC相交于O,连接C1O,则点O坐标为
(Ⅱ)设BD与AC相交于O,连接C1O,则点O坐标为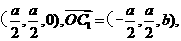
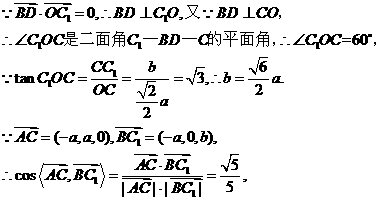 ∴异面直线BC1与AC所成角的大小为
∴异面直线BC1与AC所成角的大小为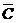 )+P(
)+P(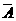 ·B·C)+P(A·
·B·C)+P(A·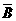 ·C)+P(A·B·C)
·C)+P(A·B·C)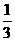 P(A·B)+
P(A·B)+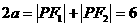 ,a=3.
,a=3.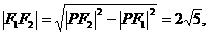 故椭圆的半焦距c=
故椭圆的半焦距c=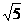 ,
,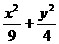 =1.
=1.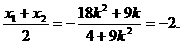
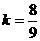 ,
,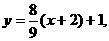
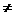 x2且
x2且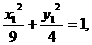 ①
①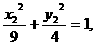 ②
②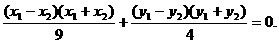 ③
③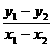 =
=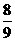 ,
,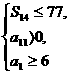 得
得 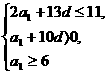 即
即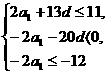
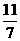 。
。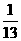

 (15)(本小题共12分)已知函数f(x)=
(15)(本小题共12分)已知函数f(x)=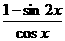 (Ⅰ)求f(x)的定义域;
(Ⅱ)设α是第四象限的角,且tan
(Ⅰ)求f(x)的定义域;
(Ⅱ)设α是第四象限的角,且tan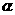 =
=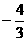 ,求f(
,求f(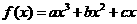 在点
在点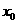 处取得极大值
处取得极大值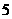 ,其导函数
,其导函数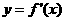 的图象经过点
的图象经过点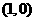 ,
,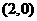 ,如图所示.求:
,如图所示.求: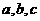 的值.
的值.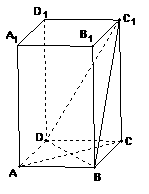 (17)(本小题共14分)
(17)(本小题共14分)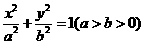 的两个焦点为F1,F2,点P在椭圆C上,且
的两个焦点为F1,F2,点P在椭圆C上,且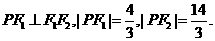
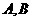 两点,且A、B关于点M对称,求直线l的方程.
两点,且A、B关于点M对称,求直线l的方程.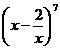 的展开式中,x3的系数是
.(用数字作答)
的展开式中,x3的系数是
.(用数字作答)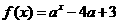 的反函数的图象经过点(-1,2),那么a的值等于 .
的反函数的图象经过点(-1,2),那么a的值等于 .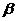 ,sin
,sin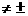 b,那么a+b与a-b的夹角的大小是
.
b,那么a+b与a-b的夹角的大小是
.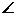 A,
A,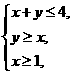 点O为坐标原点,那么|PO|的最小值等于____________,最大值等于______________.
点O为坐标原点,那么|PO|的最小值等于____________,最大值等于______________.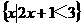 ,B=
,B=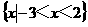 ,则A
,则A B等于
B等于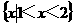 (C)
(C) 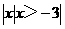 (D)
(D) 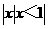
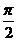 对称
对称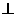 (b-c)”的
(b-c)”的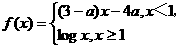 是(-
是(- ,+
,+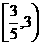 (D)(1,3)
(D)(1,3)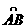 ,
,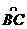 ,
,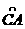 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则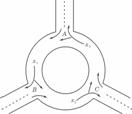
 ( 18 )(本小题共12分)
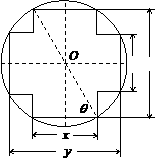
( 18 )(本小题共12分) 中,作一关于圆心对称、邻边互相
中,作一关于圆心对称、邻边互相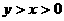 .
.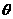 的函数;
的函数; .设数列
.设数列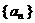 满足
满足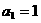 ,
,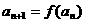 ,数列
,数列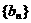 满足
满足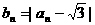 ,
,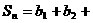 …
…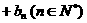 ,
, ;(Ⅱ)证明
;(Ⅱ)证明 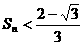 .
.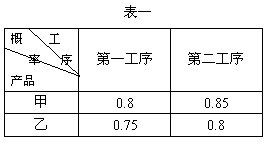 (Ⅰ)已知甲、乙两种产品每一道工序的
(Ⅰ)已知甲、乙两种产品每一道工序的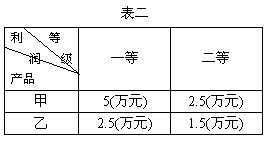 (Ⅱ)已知一件产品的利润如表二所示,用
(Ⅱ)已知一件产品的利润如表二所示,用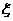 、
、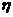 分别表示一件甲、乙产品的利润,在(Ⅰ)
分别表示一件甲、乙产品的利润,在(Ⅰ)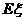 、
、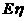 ;
;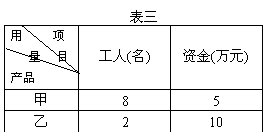 (Ⅲ)已知生产一件产品需用的工人数和资
(Ⅲ)已知生产一件产品需用的工人数和资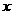 、
、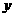 分别表示生产甲、乙产品
分别表示生产甲、乙产品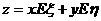 最大?最大值是多少?
最大?最大值是多少?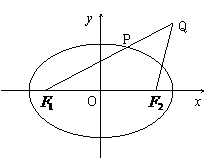 (21)(本小题满分14分)
(21)(本小题满分14分)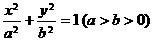 的左、右焦点分别是
的左、右焦点分别是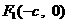 、
、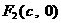 ,
,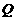 是椭圆外的动点,满足
是椭圆外的动点,满足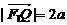 ,
,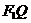 与该椭圆的交点,点T在线段
与该椭圆的交点,点T在线段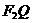 上,并且
上,并且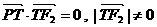 .
.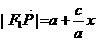 ;
;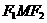 的面积
的面积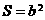 .若存在,求
.若存在,求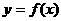 在区间
在区间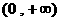 内可导,导函数
内可导,导函数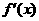 是减函数,且
是减函数,且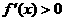 .设
.设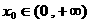 ,
,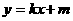 是曲线
是曲线 处的切线方程,并设函数
处的切线方程,并设函数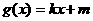 .
. 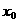 、
、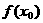 、
、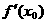 表示m;
表示m;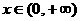 ,
,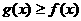 ;
;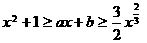 在
在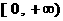 上恒成立,其中a、b为实数,求b的取值范围及a与b所满足的关系.
上恒成立,其中a、b为实数,求b的取值范围及a与b所满足的关系.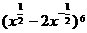 的展开式中常数项是______________.
的展开式中常数项是______________.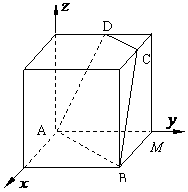 [解答]通项公式为
[解答]通项公式为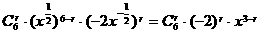 ,
,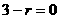 ,得
,得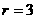 ,所以常数项是
,所以常数项是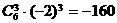 ,
,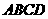 的距离是_____________.
的距离是_____________.
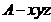 ,
,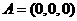 ,
,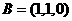 ,
,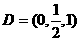 ,
,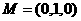 ,则
,则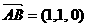 ,
,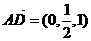 ,
,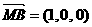 设
设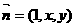 为平面
为平面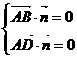 ,即
,即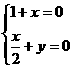 ,解得
,解得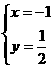 ,即
,即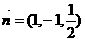 ,所以点M到截面
,所以点M到截面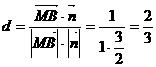 .
.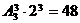 种,再将7、8插入4个空位中的两个有
种,再将7、8插入4个空位中的两个有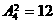 种,故有
种,故有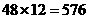 种.
种. 是正实数,设
是正实数,设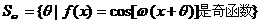 ,若对每个实数a ,
,若对每个实数a ,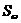 ∩
∩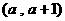 的元素不超过2个,且有a使
的元素不超过2个,且有a使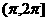
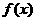 是奇函数,且
是奇函数,且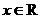 ,
,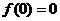 ,
,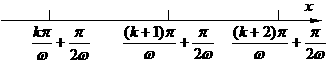 ∴
∴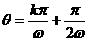 ,
,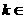 Z,
Z, ,∴
,∴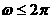 ,
,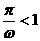 ,∴
,∴ ,∴
,∴ ,
,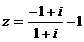 .在复平面内,z所对应的点在
(
)
.在复平面内,z所对应的点在
(
)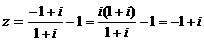
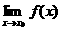 存在是函数
存在是函数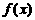 在点
在点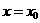 处连续的
( )
处连续的
( ) ,则函数
,则函数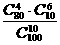 (B)
(B)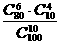 (C)
(C)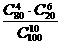 (D)
(D)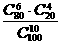
 种,其中恰有6个红球有
种,其中恰有6个红球有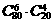 种,故选D.
种,故选D.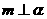 ,
,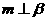 ,则
,则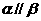 ;
;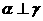 ,
,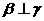 ,则
,则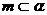 ,
,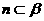 ,
,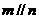 ,则
,则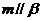 ,
,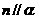 ,则
,则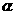 与
与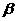 相交时,若m、n平行于两平面的交线,则
相交时,若m、n平行于两平面的交线,则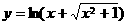 的反函数是
的反函数是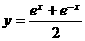 (B)
(B)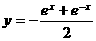 (C)
(C)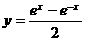 (D)
(D)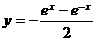
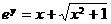 ,即
,即 ,
,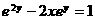 ,故
,故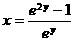 ,即
,即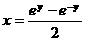 ,
,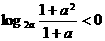 ,则a的取值范围是
,则a的取值范围是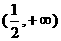 (B)
(B)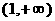 (C)
(C)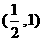 (D)
(D)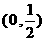
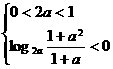 ,即
,即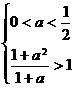 时,无解;
时,无解;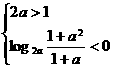 ,即
,即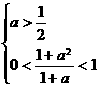 时,
时, ,故选C.
,故选C. :
: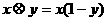 .若不等式
.若不等式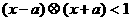 对任意实数x成立,则
对任意实数x成立,则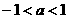 (B)
(B)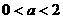 (C)
(C)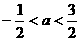 (D)
(D)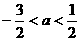
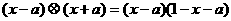 ,∴不等式
,∴不等式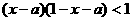 对任意实数x成立,即使
对任意实数x成立,即使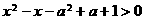 对任意实数x成立,所以
对任意实数x成立,所以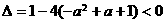 ,解得
,解得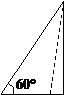 (A)
(A) (B)
(B)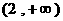 (C)
(C)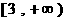 (D)
(D)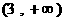
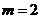 ,
,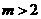 ,故选B.
,故选B.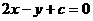 按向量
按向量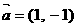 平移后与圆
平移后与圆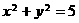 相切,则c的值为
相切,则c的值为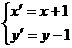 ,得
,得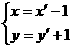 ,所以
,所以 ,其与圆
,其与圆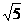 ,即
,即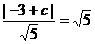 ,解得
,解得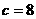 或
或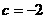 ,故选A.
,故选A.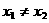 ,
,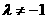 ,
,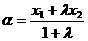 ,
,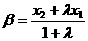 .若,则
.若,则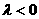 (B)
(B)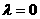 (C)
(C)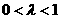 (D)
(D)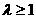
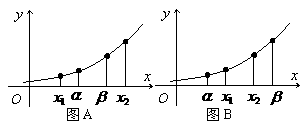 [答案]A
[答案]A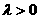 ,如图A所示,
,如图A所示,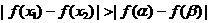 ,当
,当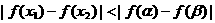 ,
,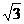 .若它的一条准线与抛物线
.若它的一条准线与抛物线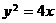 的准线重合,则
的准线重合,则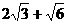 (B)
(B)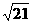 (C)
(C)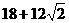 (D)21
(D)21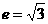 ,得
,得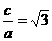 ,由一条准线与抛物线
,由一条准线与抛物线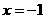 ,所以
,所以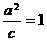 ,故
,故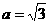 ,
,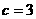 ,
,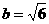 ,所以双曲线方程为
,所以双曲线方程为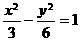 ,由
,由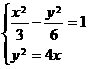 ,得交点为
,得交点为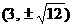 ,所以交点到原点的距离是
,所以交点到原点的距离是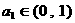 ,由关系式
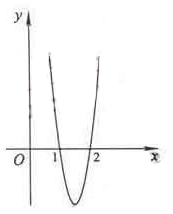
,由关系式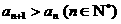 ,则该函数的图象是
,则该函数的图象是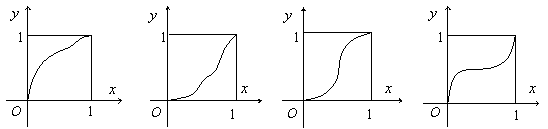
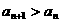 ,得
,得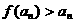 ,即
,即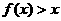 ,故选A .
,故选A .