19.(本小题满分12分)
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
(Ⅰ)证明AB⊥平面VAD;
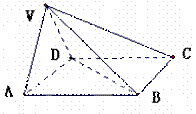 (Ⅱ)求面VAD与面VDB所成的二面角的大小.
(Ⅱ)求面VAD与面VDB所成的二面角的大小.
19.(本小题满分12分)
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
(Ⅰ)证明AB⊥平面VAD;
 (Ⅱ)求面VAD与面VDB所成的二面角的大小.
(Ⅱ)求面VAD与面VDB所成的二面角的大小.