18.解:(I)分别记“客人游览甲景点”,“客人游览乙景点”,“客人游览丙景点”
为事件A1,A2,A3. 由已知A1,A2,A3相互独立,P(A1)=0.4,P(A2)=0.5,
P(A3)=0.6.
客人游览的景点数的可能取值为0,1,2,3. 相应地,客人没有游览的景点数的可能取
值为3,2,1,0,所以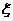 的可能取值为1,3.
的可能取值为1,3.
P(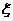 =3)=P(A1·A2·A3)+ P(
=3)=P(A1·A2·A3)+ P(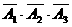 )
)
= P(A1)P(A2)P(A3)+P(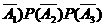 )
)
=2×0.4×0.5×0.6=0.24,
|
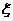 =1)=1-0.24=0.76.
=1)=1-0.24=0.76.
所以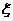 的分布列为
的分布列为
E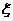 =1×0.76+3×0.24=1.48.
=1×0.76+3×0.24=1.48.
(Ⅱ)解法一 因为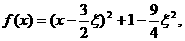
所以函数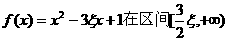 上单调递增,
上单调递增,
要使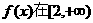 上单调递增,当且仅当
上单调递增,当且仅当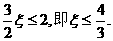
从而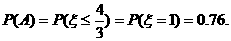
解法二: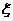 的可能取值为1,3.
的可能取值为1,3.
当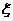 =1时,函数
=1时,函数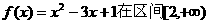 上单调递增,
上单调递增,
当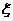 =3时,函数
=3时,函数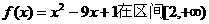 上不单调递增.0
上不单调递增.0
所以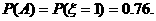
17. 解法一(I)证明 由题设知OA⊥OO1,OB⊥OO1.
解法一(I)证明 由题设知OA⊥OO1,OB⊥OO1.
所以∠AOB是所折成的直二面角的平面角,
即OA⊥OB. 故可以O为原点,OA、OB、OO1
所在直线分别为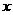 轴、y轴、z轴建立空间直角坐标系,
轴、y轴、z轴建立空间直角坐标系,
如图3,则相关各点的坐标是A(3,0,0),
B(0,3,0),C(0,1,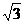 )
)
|
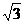 ).
).
从而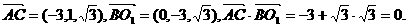
所以AC⊥BO1.
(II)解:因为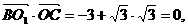 所以BO1⊥OC,
所以BO1⊥OC,
由(I)AC⊥BO1,所以BO1⊥平面OAC,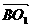 是平面OAC的一个法向量.
是平面OAC的一个法向量.
设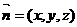 是0平面O1AC的一个法向量,
是0平面O1AC的一个法向量,
由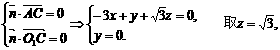 得
得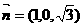 .
.
设二面角O-AC-O1的大小为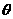 ,由
,由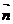 、
、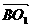 的方向可知
的方向可知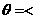
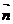 ,
,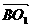 >,
>,
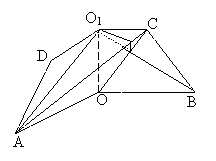 所以cos
所以cos
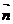 ,
,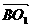 >=
>=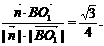
即二面角O-AC-O1的大小是
解法二(I)证明 由题设知OA⊥OO1,OB⊥OO1,
所以∠AOB是所折成的直二面角的平面角,
|
OC是AC在面OBCO1内的射影.
因为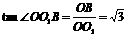
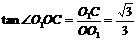 ,
,
所以∠OO1B=60°,∠O1OC=30°,从而OC⊥BO1
由三垂线定理得AC⊥BO1.
(II)解 由(I)AC⊥BO1,OC⊥BO1,知BO1⊥平面AOC.
设OC∩O1B=E,过点E作EF⊥AC于F,连结O1F(如图4),则EF是O1F在平面AOC
内的射影,由三垂线定理得O1F⊥AC.
所以∠O1FE是二面角O-AC-O1的平面角.
由题设知OA=3,OO1=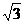 ,O1C=1,
,O1C=1,
所以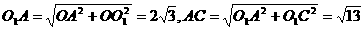 ,
,
从而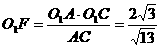 , 又O1E=OO1·sin30°=
, 又O1E=OO1·sin30°=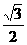 ,
,
所以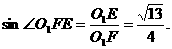 即二面角O-AC-O1的大小是
即二面角O-AC-O1的大小是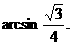
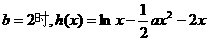 ,
,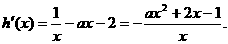
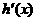 <0有解.
<0有解.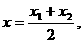
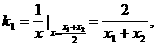
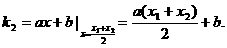
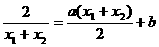 ,则
,则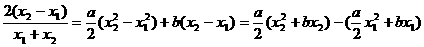
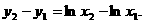
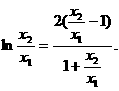 设
设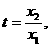 则
则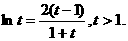 ①
①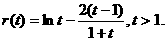 则
则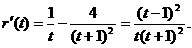
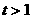 时,
时,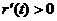 ,所以
,所以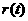 在
在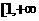 )上单调递增. 故
)上单调递增. 故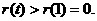
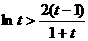 . 这与①矛盾,假设不成立.
. 这与①矛盾,假设不成立.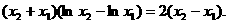
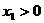 ,所以
,所以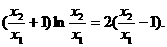
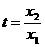 ,得
,得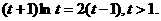 ②
②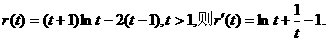
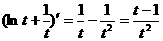 ,所以
,所以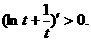
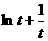 在[1,+
在[1,+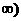 上单调递增.从而
上单调递增.从而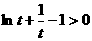 ,即
,即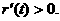
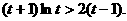 这与②矛盾,假设不成立.
这与②矛盾,假设不成立.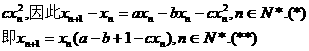
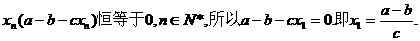
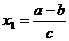 时,每年年初鱼群的总量保持不变.
时,每年年初鱼群的总量保持不变.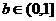
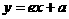 与x轴、y轴的交点,所以A、B的坐标分别是
与x轴、y轴的交点,所以A、B的坐标分别是 .
.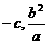 ). 由
). 由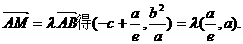

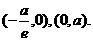 设M的坐标是
设M的坐标是
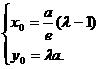 因为点M在椭圆上,所以
因为点M在椭圆上,所以 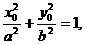
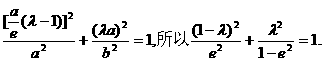
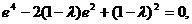 解得
解得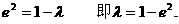
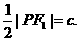
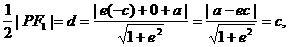
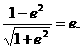 所以
所以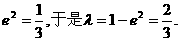
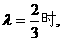 △PF1F2为等腰三角形.
△PF1F2为等腰三角形.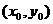 ,
,
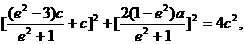
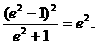 从而
从而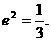
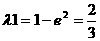 . 即当
. 即当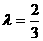 时,△PF1F2为等腰三角形.
时,△PF1F2为等腰三角形.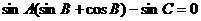
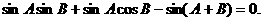
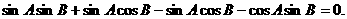
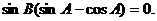
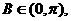 所以
所以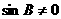 ,从而
,从而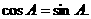
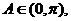 知
知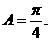 从而
从而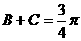 .
.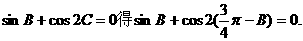
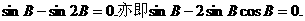
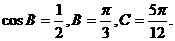 所以
所以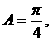
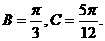
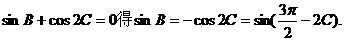
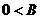 、
、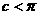 ,所以
,所以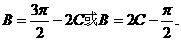
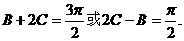
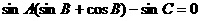 得
得 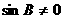 ,所以
,所以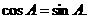
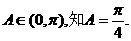 从而
从而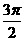 不合要求.
不合要求.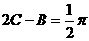 ,得
,得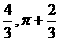
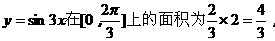
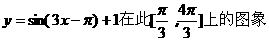
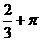 .
.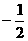
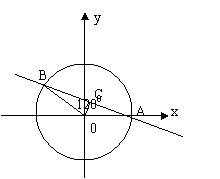 [解析]:如图
[解析]:如图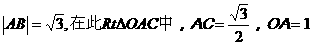
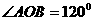
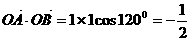 .
. .
.