0 446811 446819 446825 446829 446835 446837 446841 446847 446849 446855 446861 446865 446867 446871 446877 446879 446885 446889 446891 446895 446897 446901 446903 446905 446906 446907 446909 446910 446911 446913 446915 446919 446921 446925 446927 446931 446937 446939 446945 446949 446951 446955 446961 446967 446969 446975 446979 446981 446987 446991 446997 447005 447348
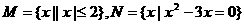 ,则M∩N
,则M∩N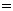 ( )
( )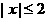 ,得
,得 ,
,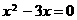 ,得
,得 ,
,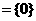 ,故选B.
,故选B. ,其中a、b∈R,i是虚数单位,则
,其中a、b∈R,i是虚数单位,则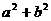 = ( )
= ( )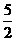 D.5
D.5 ,∴
,∴ ,
,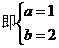 ,
,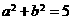 ,故选D.
,故选D.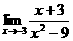 = ( )
= ( )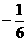 B.0 C.
B.0 C. D.
D.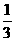
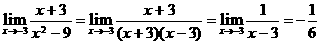 ,故选A.
,故选A. ( 4 ) 已知高为3的直棱锥
( 4 ) 已知高为3的直棱锥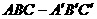 的底面是边长为1的正三角形
的底面是边长为1的正三角形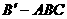 的体积为
( )
的体积为
( ) B.
B.
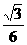 D.
D.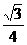
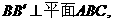
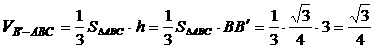 .
.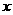 轴上的椭圆
轴上的椭圆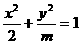 的离心率为
的离心率为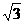 B.
B.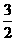 C.
C.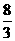 D.
D.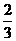
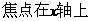 ,∴
,∴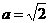 ,
,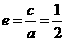 ,∴
,∴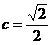 ,
,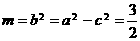 ,故选B.
,故选B.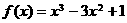 是减函数的区间为 ( )
是减函数的区间为 ( )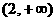 B.
B. C.
C. D.(0,2)
D.(0,2)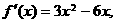
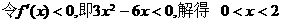 ,故选D.
,故选D. 、
、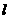 、
、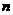 和平面
和平面 、
、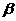 ,的四个命题:
,的四个命题: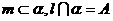 ,点
,点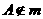 ,则
,则 , 且
, 且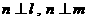 ,则
,则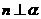 ;
; ,
, 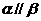 ,则
,则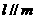 ;
;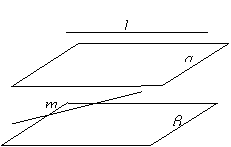 ④若
④若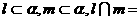 点
点 ,
,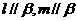 ,则
,则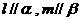 ,
, 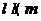 ,故选C.
,故选C.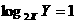 的概率为 ( )
的概率为 ( )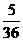 C.
C.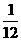 D.
D.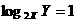 的X、Y有(1, 2),(2, 4),(3, 6)这3种情况,而总的可能数有36种,所以
的X、Y有(1, 2),(2, 4),(3, 6)这3种情况,而总的可能数有36种,所以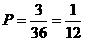 ,故选C.
,故选C.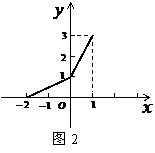
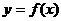 和
和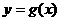 的图像
的图像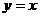 对称.现将
对称.现将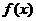 的表达式为
的表达式为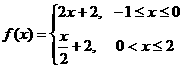 B.
B.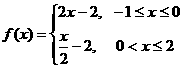
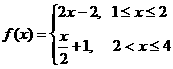 D.
D.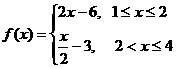
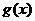 的图象,故
的图象,故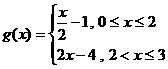 ,
,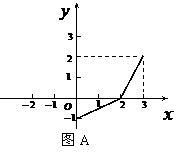 ∵函数
∵函数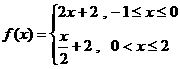 ,故选A.
,故选A.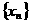 满足
满足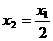 ,
,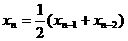 ,
,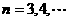 .若
.若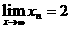 ,则
,则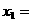
 时,
时,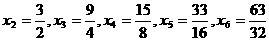
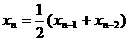 ,∴
,∴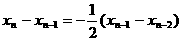 ,
,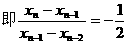 ,
,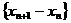 是以(
是以(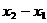 )为首项,以
)为首项,以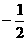 为公比6的等比数列,
为公比6的等比数列, ,则
,则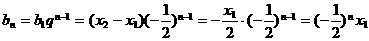
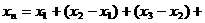 …
…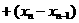
 …
…
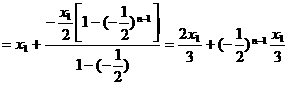
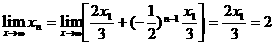 ,∴
,∴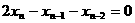 ,
,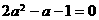 ,
,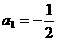 ,
,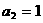 ,
,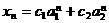 ,
,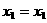 ,
,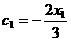 ,
,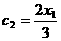 ,
,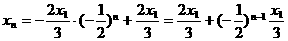 ,以下同解法二.
,以下同解法二.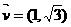 的直线l过点(
的直线l过点(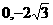 )和椭圆
)和椭圆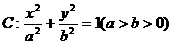 的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.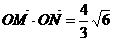 cot
cot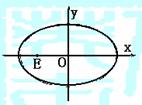
 ,
①
,
①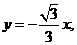 ②
②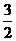 .∵椭圆中心O(0,0)关于直线ι的对称点在椭圆C的右准线上,
.∵椭圆中心O(0,0)关于直线ι的对称点在椭圆C的右准线上, .∵直线ι过椭圆焦点,∴该焦点坐标为(2,0).
.∵直线ι过椭圆焦点,∴该焦点坐标为(2,0). . ③
. ③ ,x1x2=
,x1x2= ,
,
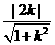 .∵
.∵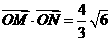 cot∠MON,即
cot∠MON,即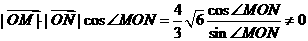 ,
, ,∴
,∴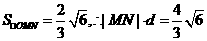 ,
,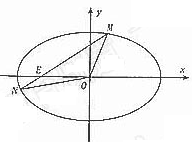
 即
即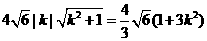 .整理得
.整理得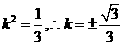 .
.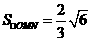
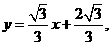 或y=
或y=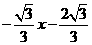 或x=-2.
或x=-2.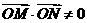 .
.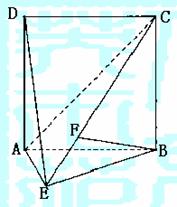 (Ⅰ)求证AE⊥平面BCE;
(Ⅰ)求证AE⊥平面BCE;
 ,
,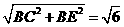 ,BF=
,BF=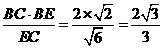
 ,∴二面角B-AC-E等于arcsin
,∴二面角B-AC-E等于arcsin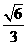 .
.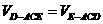 ,∴
,∴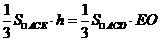 .
.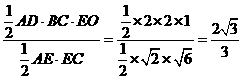 .
.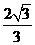 .
.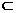 面BCE,∴AE⊥BE,在直角三角形AEB中,AB=2,O为AB的中点
面BCE,∴AE⊥BE,在直角三角形AEB中,AB=2,O为AB的中点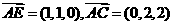
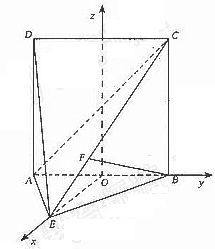
 =(x,y,z),则
=(x,y,z),则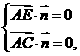 即
即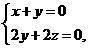 解得
解得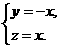
 =(1,0,0),
=(1,0,0),
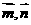 )=
)=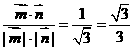
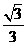 .
.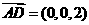 ,∴点D到平面ACE的距离
,∴点D到平面ACE的距离 |
|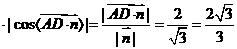 .
.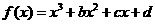 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为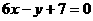 .
. 的解析式;
的解析式;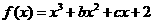 ,
,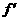 (x)=3x2+2bx+c,由在(-1,(-1))处的切线方程是6x-y+7=0,知
(x)=3x2+2bx+c,由在(-1,(-1))处的切线方程是6x-y+7=0,知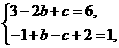 即
即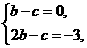 解得b=c=-3.
解得b=c=-3. }是公比为q的等比数列,且
}是公比为q的等比数列,且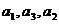 成等差数列.
成等差数列.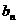 }是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.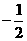
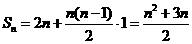 .
.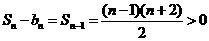 ,故
,故
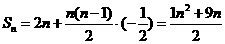 ,
,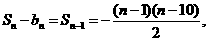 ,
,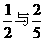 .
.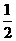 ,P(B)=
,P(B)=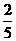 ,P(
,P( )=
)=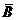 )=
)=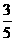
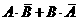
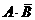 )+P(
)+P(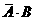 )=
)=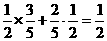
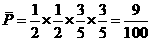
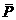 =1-
=1-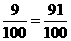

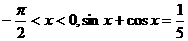 .
.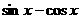 的值;
的值;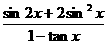 的值.
的值.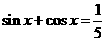 ,得
,得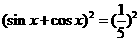 ,得2sinxcosx=
,得2sinxcosx= ,∵(sinx-cosxx)2=1-2sinxcosx=
,∵(sinx-cosxx)2=1-2sinxcosx=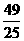 ,又
,又 ∴sinx<0cosx>0,∴sinx-cosx=-
∴sinx<0cosx>0,∴sinx-cosx=-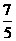
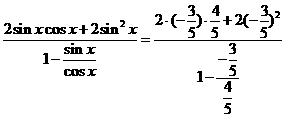 =
=
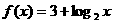 的图象与
的图象与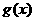 的图象关于
对称,则函数
的图象关于
对称,则函数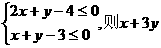 的最大值为
.
的最大值为
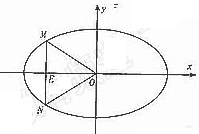
. 如右图,在同一平面直角坐标系中画出下列
如右图,在同一平面直角坐标系中画出下列 表示的区域为DMAO,
表示的区域为DMAO,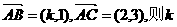 的值是
.
的值是
.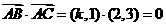 ,得k=
,得k=