摘要:已知函数f(x)= (Ⅰ)求f(x)的定义域, (Ⅱ)设α是第四象限的角.且tan=.求f()的值. 已知函数在点处取得极大值.其导函数的图象经过点..如图所示.求: (Ⅰ)的值, (Ⅱ)的值. 如图.ABCD-A1B1C1D1是正四棱柱. (Ⅰ)求证:BD⊥平面ACC1A1; (Ⅱ)]若二面角C1-BD-C的大小为60o,求异面直线BC1与AC所成角的大小. 某公司招聘员工.指定三门考试课程.有两种考试方案. 方案一:考试三门课程.至少有两门及格为考试通过, 方案二:在三门课程中.随机选取两门.这两门都及格为考试通过. 假设某应聘者对三门指定课程考试及格的概率分别是0.5.0.6.0.9.且三门课程考试是否及格相互之间没有影响.求: (Ⅰ)该应聘者用方案一考试通过的概率, (Ⅱ)该应聘者用方案二考试通过的概率. 椭圆C:的两个焦点为F1,F2,点P在椭圆C上.且 (Ⅰ)求椭圆C的方程, (Ⅱ)若直线l过圆x2+y2+4x-2y=0的圆心.交椭圆C于两点.且A.B关于点M对称.求直线l的方程. 设等差数列{an}的首项a1及公差d都为整数.前n项和为Sn. (Ⅰ)若a11=0,S14=98,求数列{an}的通项公式, (Ⅱ)若a1≥6.a11>0.S14≤77.求所有可能的数列{an}的通项公式. 答案:
网址:http://m.1010jiajiao.com/timu3_id_4469516[举报]
(本小题共12分)
已知函数f(x)=2x- -aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间;
-aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间;
(2)求y=f(x)的极值点(即函数取到极值时点的横坐标).
查看习题详情和答案>>
(本小题12分)
已知函数f(x)= x
x -(2a+1)x
-(2a+1)x +3a(a+2)x+
+3a(a+2)x+ ,其中a为实数。
,其中a为实数。
(1)当a=-1时,求函数y=f(x)在[0,6]上的最大值与最小值;
(2)当函数y=f (x)的图像在(0,6)上与x轴有唯一的公共点时,求实数a的取值范围。
(x)的图像在(0,6)上与x轴有唯一的公共点时,求实数a的取值范围。
查看习题详情和答案>>

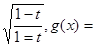
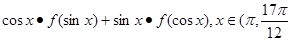 ]
]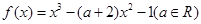 ,
,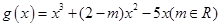 的图像与函数
的图像与函数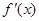 的图像恰好有三个不同的交点,若存在,请求出实数m的取值范
的图像恰好有三个不同的交点,若存在,请求出实数m的取值范 围;若不存在,请说明理由。
围;若不存在,请说明理由。 的部分图象
如图所示,求f(x)的解析式.
的部分图象
如图所示,求f(x)的解析式.