0 446823 446831 446837 446841 446847 446849 446853 446859 446861 446867 446873 446877 446879 446883 446889 446891 446897 446901 446903 446907 446909 446913 446915 446917 446918 446919 446921 446922 446923 446925 446927 446931 446933 446937 446939 446943 446949 446951 446957 446961 446963 446967 446973 446979 446981 446987 446991 446993 446999 447003 447009 447017 447348
 ,且
,且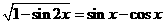 ,则 ( )
,则 ( )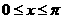 B.
B.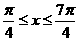 C.
C.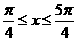 D.
D.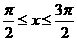
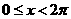 ,
,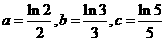 ,则 ( )
,则 ( )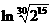 ,b=
,b=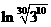 ,c=
,c=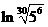 ,
,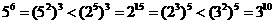 ,∴c<a<b,选C
,∴c<a<b,选C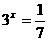 ,则 ( )
,则 ( )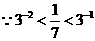 ,
,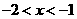 ,选A
,选A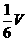 B.
B.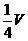 C.
C.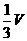 D.
D.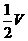
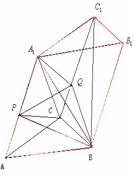 解:如图,
解:如图,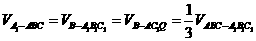
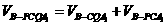 ,∵AF=QC1,
,∵AF=QC1,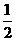 (
(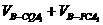 )
)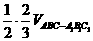 =
=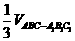 ,选C
,选C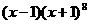 的展开式中
的展开式中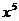 的系数是 ( )
的系数是 ( )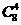 ,
,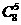 ,∴(x-1)(x+1)8展开式中x5的系数为
,∴(x-1)(x+1)8展开式中x5的系数为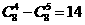 ,选B
,选B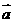 =(1,-2),
=(1,-2),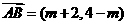 ,由
,由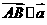
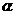 为第三象限角,则
为第三象限角,则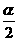 所在的象限是 ( )
所在的象限是 ( )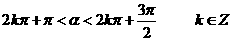 ,
,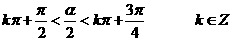 ,可知
,可知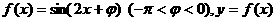 图像的一条对称轴是直线
图像的一条对称轴是直线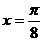 。
。 ;
; 的单调增区间;
的单调增区间;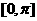 上的图像。
上的图像。
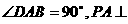 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=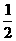 AB=1,M是PB的中点。
AB=1,M是PB的中点。 的二次项系数为
的二次项系数为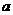 ,且不等式
,且不等式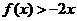 的解集为
的解集为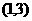 。
。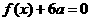 有两个相等的根,求
有两个相等的根,求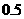 ,若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种。
,若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种。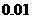 )
)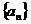 的首项
的首项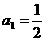 ,前n项和为
,前n项和为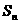 ,且
,且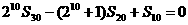 。
。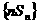 的前n项和
的前n项和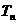 。
。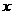 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,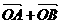 与
与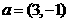 共线。
共线。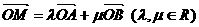 ,证明
,证明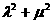 为定值。
为定值。





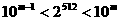 ,则m = 。
,则m = 。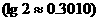
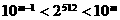 ,∴
,∴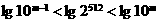 ,即
,即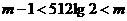 ,
,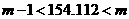 ,即
,即 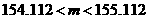 ,∴
,∴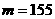 .
.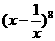 的展开式中,常数项为
。(用数字作答
的展开式中,常数项为
。(用数字作答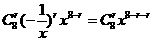 ,令8-2r=0,得r=4,∴常数项为70.
,令8-2r=0,得r=4,∴常数项为70.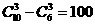 ,∴从6名男生和4名女生中,选出3名代表,要求至少包含1名女生,则不同的选法共有100种。
,∴从6名男生和4名女生中,选出3名代表,要求至少包含1名女生,则不同的选法共有100种。 中,过对角线
中,过对角线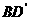 的一个平面交
的一个平面交 于E,交
于E,交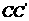 于F,
于F,  一定是平行四边形
一定是平行四边形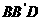
 解:①平面
解:①平面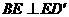 ,又
,又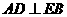 ,
,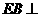 平面
平面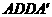 ,产生矛盾;
,产生矛盾;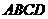 ;
;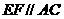 ,又
,又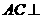 平面
平面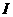 为全集,
为全集,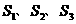 是
是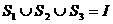 ,则下面论断正确的是
,则下面论断正确的是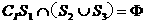 (B)
(B)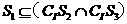
 (C)
(C)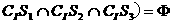 (D)
(D)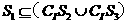
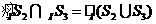 所表示的部分是图中蓝色
所表示的部分是图中蓝色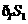 所表示的部分是图中除去
所表示的部分是图中除去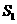 的部分,
的部分,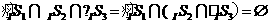 ,故选C.
,故选C.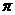 ,则球的表面积为
,则球的表面积为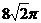 (B)
(B)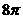 (C)
(C)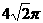 (D)
(D)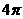
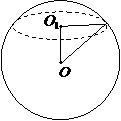 解:∵截面圆面积为
解:∵截面圆面积为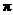 ,∴截面圆半径
,∴截面圆半径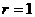 ,
,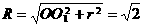 ,
,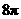 ,故选B.
,故选B.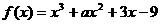 ,已知
,已知 时取得极值,则
时取得极值,则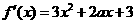 ,令
,令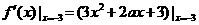 =0,解得a=5,选(D)
=0,解得a=5,选(D) 均为正三角形,EF∥AB,EF=2,则该多面体的体积为
均为正三角形,EF∥AB,EF=2,则该多面体的体积为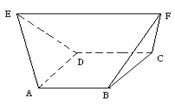 (A)
(A)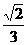 (B)
(B)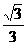
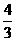 (D)
(D)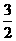

 ,∵
,∵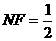 ,
,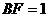 ,∴
,∴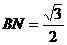 ,
,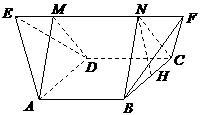 作NH垂直于点H,则H为BC的中点,则
作NH垂直于点H,则H为BC的中点,则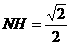 ,∴
,∴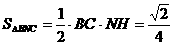 ,∴
,∴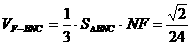 ,
,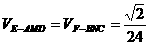 ,
,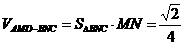 ,∴
,∴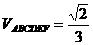 ,故选A.
,故选A.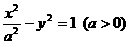 的一条准线为
的一条准线为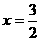 ,则该双曲线的离心率为
,则该双曲线的离心率为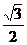 (B)
(B)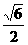 (D)
(D)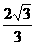
 ,∴
,∴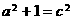 ,抛物线
,抛物线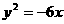 的准线为
的准线为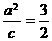 ,解得
,解得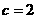 ,所以
,所以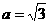 ,所以离心率为
,所以离心率为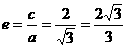 ,故选D.
,故选D.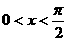 时,函数
时,函数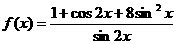 的最小值为
的最小值为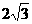 (C)4 (D)
(C)4 (D)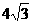
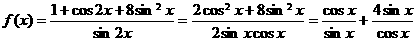
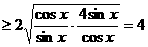 ,当且仅当
,当且仅当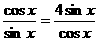 ,即
,即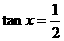 时,取“
时,取“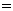 ”,∵
”,∵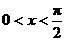 ,∴存在
,∴存在 ,故选(C).
,故选(C).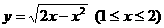 反函数是
反函数是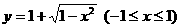
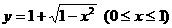
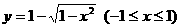
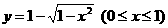
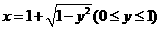 ,故
,故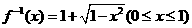 ,选(D)
,选(D) ,函数
,函数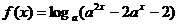 ,则使
,则使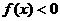 的
的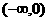 (B)
(B)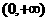 (C)
(C)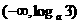 (D)
(D)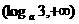
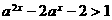 ,解得
,解得 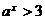 或
或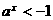 (舍去),
(舍去),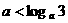 ,故选C.
,故选C.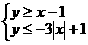 所表示的平面区域的面积为
所表示的平面区域的面积为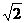 (B)
(B)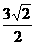 (D)2
(D)2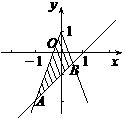 解:原不等式化为
解:原不等式化为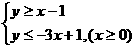 或
或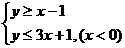 ,
,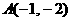 ,
,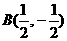 ,
,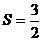 ,故选B
,故选B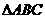 中,已知
中,已知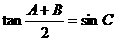 ,给出以下四个论断:
,给出以下四个论断: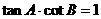 ②
②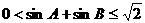
 ④
④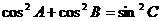
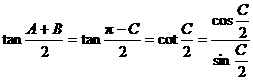 ,
,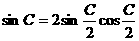 ,
,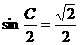 ,∴
,∴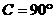 ,
,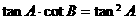 ,∴①不一定成立,
,∴①不一定成立,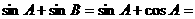
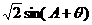 ,∴
,∴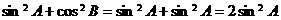 ,∴③不一定成立,
,∴③不一定成立,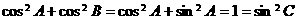 ,∴④成立,故选B.
,∴④成立,故选B.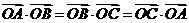 ,则点O是
,则点O是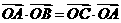 ,
,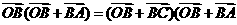
 ,故
,故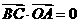 ,
,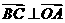 ,同理可证
,同理可证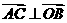 ,∴O是
,∴O是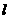 过点
过点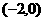 ,且与圆
,且与圆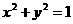 相切,则
相切,则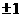 (B)
(B)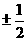 (C)
(C)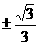 (D)
(D)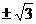
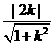 得k=
得k=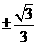 ,选(D).
,选(D).