17.(本小题共13分)
甲、乙两人各进行3次射击,甲每次击中目标的概率为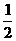 ,乙每次击中目标的概率为
,乙每次击中目标的概率为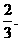
(Ⅰ)记甲击中目标的次数为ξ,求ξ的概率分布及数学期望Eξ;
(Ⅱ)求乙至多击中目标2次的概率;
(Ⅲ)求甲恰好比乙多击中目标2次的概率.
[答案]
[详解]
解:(I)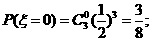
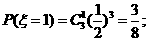
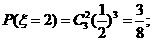
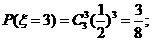
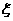 的概率分布如下表:
的概率分布如下表:
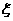 |
0 |
1 |
2 |
3 |
|
P |
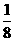 |
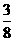 |
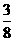 |
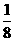 |
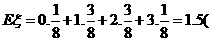 或
或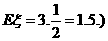
(II)乙至多击中目标2次的概率为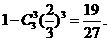
(III)设甲恰比乙多击中目标2次为事件A,甲恰击中目标2次且乙恰击中目标0次
为事件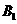 ,甲恰击中目标3次且乙恰击中目标1次为事件
,甲恰击中目标3次且乙恰击中目标1次为事件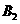 ,则
,则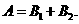
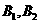 为互斥事件.
为互斥事件.
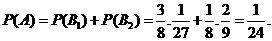
所以,甲恰好比乙多击中目标2次的概率为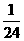 .
.
[名师指津]
概率应用题在每年的各地高考试题中基本上都会有所涉及,而且本类题相对比较容易解决,复习时一定将这类题落实.
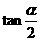 =2,求
=2,求 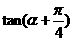 的值; (II)
的值; (II) 的值.
的值.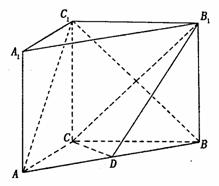 (16)(本小题共14分)
(16)(本小题共14分)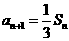 ,n=1,2,3,……,求
,n=1,2,3,……,求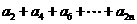 的值.
的值.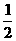 ,乙每次击中目标的概率
,乙每次击中目标的概率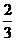 ,
,
 的展开式中的常数项是
(用数字作答)
的展开式中的常数项是
(用数字作答)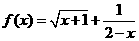 的定义域为
.
的定义域为
.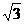 ,∠A=45°,∠C=75°,则BC的长为
.
,∠A=45°,∠C=75°,则BC的长为
.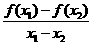 >0;④
>0;④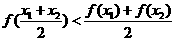 .
.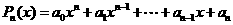 ,
,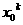 (k=2,3,4,…,n)的值需要k-1次乘法,计算
(k=2,3,4,…,n)的值需要k-1次乘法,计算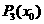 的值共需要9次运算(6次乘法,3次加法),那么计算
的值共需要9次运算(6次乘法,3次加法),那么计算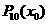 的值共需要
次运算.
的值共需要
次运算.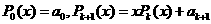 (k=0, 1,2,…,n-1).利用该算法,计算
(k=0, 1,2,…,n-1).利用该算法,计算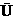 M (C)M
M (C)M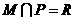
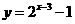 的图象,只需把函数
的图象,只需把函数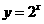 上所有点
上所有点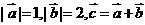 ,且
,且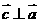 ,则向量
,则向量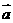 与
与 的夹角为
的夹角为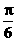 (B)
(B)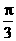 (C)
(C) (D)
(D)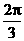
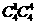 种 (B)
种 (B)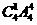 种 (C)
种 (C)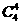 种 (D)
种 (D)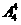 种
种 是定义在[0,1]上的函数,若存在
是定义在[0,1]上的函数,若存在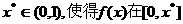 上单调递增,在[x*,1]上单调递减,则称
上单调递增,在[x*,1]上单调递减,则称 为含峰区间;
为含峰区间;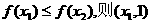 为含峰区间;
为含峰区间;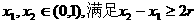 ,使得由(Ⅰ)所确定的含峰区间的长度不大于0.5+r;
,使得由(Ⅰ)所确定的含峰区间的长度不大于0.5+r;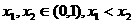 ,由(Ⅰ)可确定含峰区间为(0,
,由(Ⅰ)可确定含峰区间为(0, )或(
)或(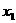 ,1),在所得的含峰区间内选取
,1),在所得的含峰区间内选取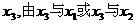 类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0,
类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0, 的值,满足两两之差的绝地值不小于0.02,且使得新的含峰区间的长度缩短到0.34.
的值,满足两两之差的绝地值不小于0.02,且使得新的含峰区间的长度缩短到0.34.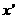 为
为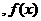 在
在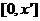 上单调递增,
上单调递增,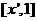 上单调递减.
上单调递减.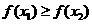 时,假设
时,假设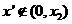 ,则
,则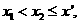 从而
从而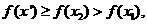
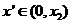 ,即
,即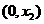 是含峰区间.
是含峰区间.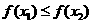 时,假设
时,假设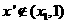 ,则
,则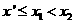 ,从而
,从而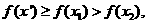
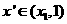 ,即
,即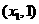 是含峰区间.
是含峰区间.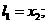
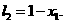
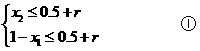
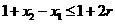 ,即
,即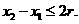
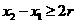 ,所以
,所以
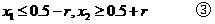
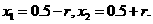
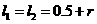 ,即存在
,即存在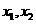 使得所确定的含峰区间
使得所确定的含峰区间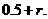
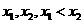 ,由(II)可知
,由(II)可知
 的取值应满足
的取值应满足
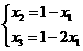
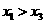 时,含峰区间的长度为
时,含峰区间的长度为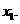
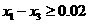 ,得
,得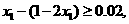 ,从而
,从而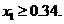
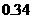 ,只要取
,只要取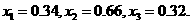
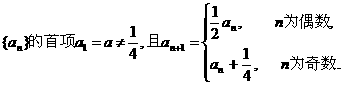
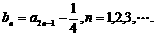
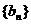 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;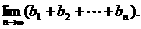
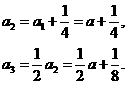
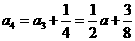 ,所以
,所以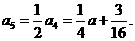
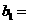
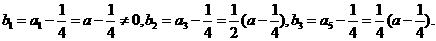
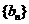 是公比为
是公比为 的等比数列.
的等比数列.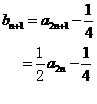
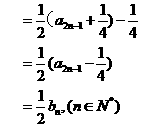
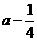 ,公比为
,公比为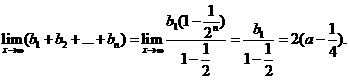
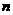 项和公式的求法和运用,等差等比数列的性质做为本
项和公式的求法和运用,等差等比数列的性质做为本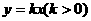 与直线l2:
与直线l2: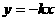 之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.
之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.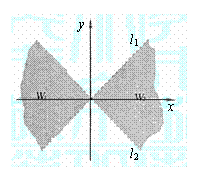
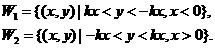
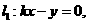 直线
直线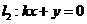 ,由题意得
,由题意得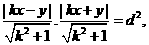
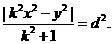
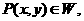 知
知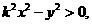
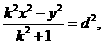 即
即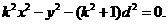
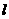 与
与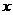 轴垂直时,可设直线
轴垂直时,可设直线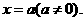 由于直线
由于直线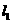 与
与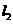 关于
关于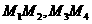 的中点坐标都为
的中点坐标都为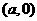 ,所以
,所以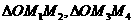
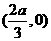 ,即它们的重心重合.
,即它们的重心重合.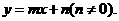
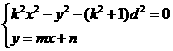 ,得
,得
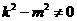 ,且
,且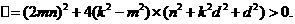
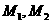 的坐标分别为
的坐标分别为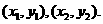
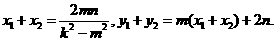
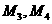 的坐标分别为
的坐标分别为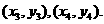
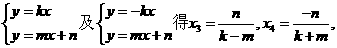
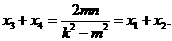
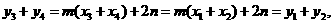
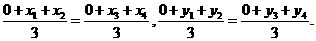
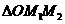 的重心与
的重心与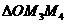 的重心也重合.
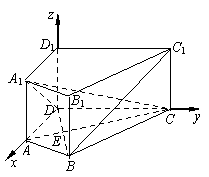
的重心也重合. 如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=
如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=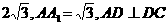 ,
,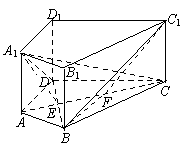 解法一:
解法一: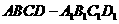 中,
中,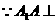 底面
底面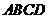 ,
, 是
是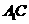 在平面
在平面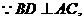
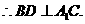
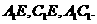
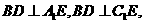
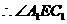 为二面角
为二面角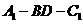 的平面角.
的平面角.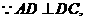
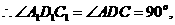
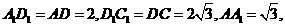 且
且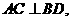
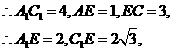
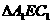 中,
中,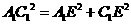 ,
, 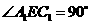 ,
,
 于
于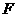 ,连结
,连结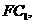
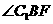 就是
就是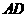 与
与 所成的角.
所成的角.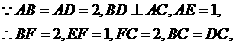

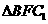 中,
中,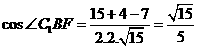 。
。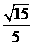 。
。 解法二:
解法二: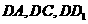 所
所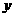 轴,
轴,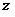 轴,建立空间
轴,建立空间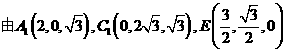
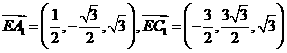 。
。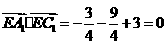 。∴
。∴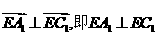 。
。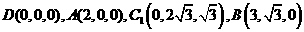 ,得
,得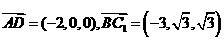 。
。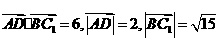 ,
,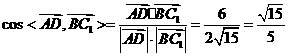 。
。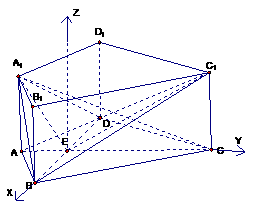 (II)如图,建立空间直角坐标,坐标原点为E.
(II)如图,建立空间直角坐标,坐标原点为E.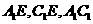
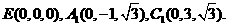
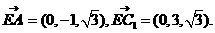
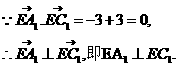
 二面角
二面角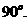
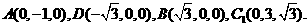

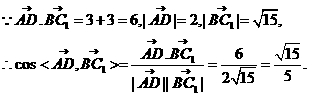
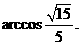
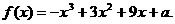
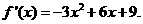
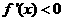 ,解得
,解得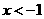 或
或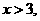
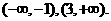
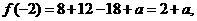
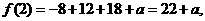
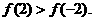
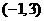 上
上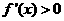 ,所以
,所以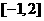 单调递增,又由于
单调递增,又由于 上单调递减,因此
上单调递减,因此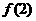 和
和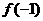 分别是
分别是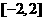 上的最大值和最小值.
上的最大值和最小值.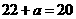 ,解得
,解得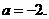
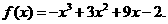
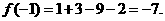
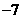
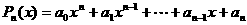 .
.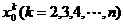 的值需要k-1次乘法,计算P3(x0)的值共需要9次运算(6次乘法,3次加法),那么计算P10(x0)的值共需要
的值需要k-1次乘法,计算P3(x0)的值共需要9次运算(6次乘法,3次加法),那么计算P10(x0)的值共需要
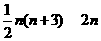
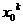 的值需要
的值需要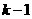 次运算,即进行
次运算,即进行 的乘法运算可得到
的乘法运算可得到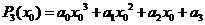 这里
这里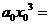
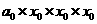 进行了3次运算,
进行了3次运算,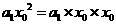 进行了2次运算,
进行了2次运算,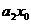 进行1次运算,最后
进行1次运算,最后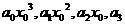 之间的加法
之间的加法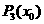 总共进行了
总共进行了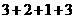
 次运算
次运算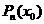
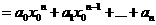 总共进行了
总共进行了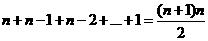 次
次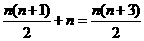 次
次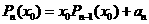 ,
,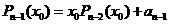
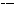
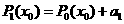 ,
,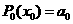
 次
次