18.(本小题满分14分)
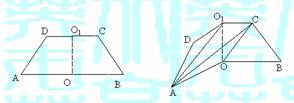 如图1,已知ABCD是上.下底边长分别为2和6,高为
如图1,已知ABCD是上.下底边长分别为2和6,高为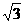 的等腰梯形,将它沿对称轴OO1折成直二面角,如图2.
的等腰梯形,将它沿对称轴OO1折成直二面角,如图2.
(Ⅰ)证明:AC⊥BO1;
(Ⅱ)求二面角O-AC-O1的大小.
|
18.(本小题满分14分)
 如图1,已知ABCD是上.下底边长分别为2和6,高为
如图1,已知ABCD是上.下底边长分别为2和6,高为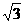 的等腰梯形,将它沿对称轴OO1折成直二面角,如图2.
的等腰梯形,将它沿对称轴OO1折成直二面角,如图2.
(Ⅰ)证明:AC⊥BO1;
(Ⅱ)求二面角O-AC-O1的大小.
|