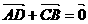0 446856 446864 446870 446874 446880 446882 446886 446892 446894 446900 446906 446910 446912 446916 446922 446924 446930 446934 446936 446940 446942 446946 446948 446950 446951 446952 446954 446955 446956 446958 446960 446964 446966 446970 446972 446976 446982 446984 446990 446994 446996 447000 447006 447012 447014 447020 447024 447026 447032 447036 447042 447050 447348
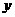 =
=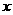 +
+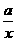 有如下性质:如果常数
有如下性质:如果常数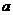 >0,那么该函数在
>0,那么该函数在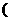 0,
0,
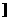 上是减函数,在
上是减函数,在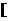
 上是增函数.
上是增函数.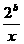 (
(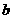 的值;
的值;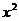 +
+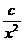 (常数
(常数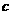 >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;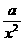 (常数
(常数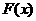 =
=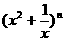 +
+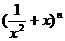 (
(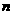 是正整数)在区间[
是正整数)在区间[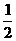 ,2]上的最大值和最小值(可利用你的研究结论).
,2]上的最大值和最小值(可利用你的研究结论).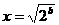 时,
时,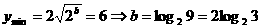 。
。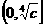 上是减函数,在
上是减函数,在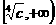 上是增函数;则该函数在
上是增函数;则该函数在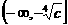 上是减函数,在
上是减函数,在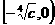 上是增函数。
上是增函数。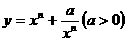 ,当
,当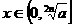 ,
,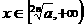 ,
,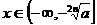 ,
,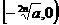 ,
,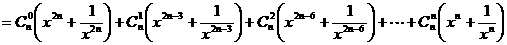
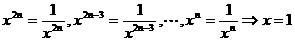 时,
时,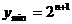 。
。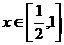 ,
,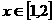 ,
,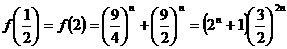
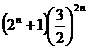 ,最小值为
,最小值为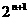 。
。
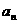
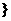 共有2
共有2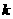 项(整数
项(整数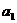 =2.设该数列的前
=2.设该数列的前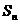 ,且
,且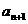 =
=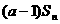 +2(
+2(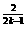 ,数列
,数列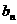
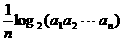 (
(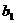 -
-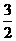 |+|
|+|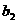 -
-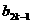 -
-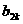 -
-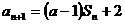 ,则
,则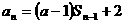 ,两式相减,得
,两式相减,得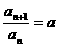 ,
,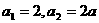 )
)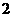 、公比为
、公比为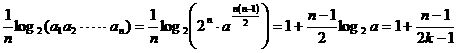 ,(
,(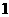 、公差为
、公差为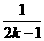 的等差数列。
的等差数列。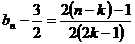 ,∴
,∴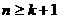 时,
时,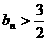 ;
;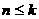 时,
时,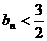 。
。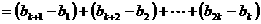
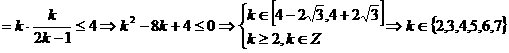 。
。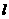 与抛物线
与抛物线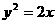 相交于
相交于 、
、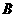 两点。
两点。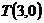 ,那么
,那么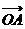
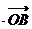 =
=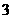 ”是真命题;
”是真命题;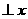 轴,则
轴,则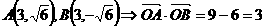
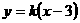 ,
,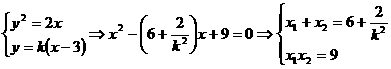
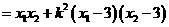
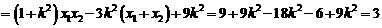
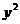 =2
=2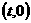 ,则直线方程为
,则直线方程为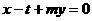 ,把它代入
,把它代入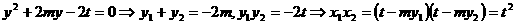
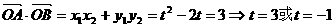 ,即直线
,即直线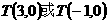 。
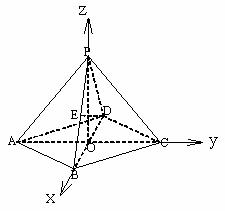
。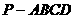 中,底面是边长为
中,底面是边长为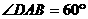 ,对角线
,对角线 与
与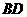 相交于点
相交于点 ,
,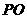 ⊥平面
⊥平面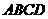 ,
,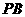 与平面
与平面 .
.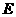 是
是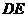 与
与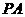 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).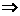
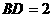
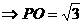 ,
,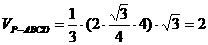 。
。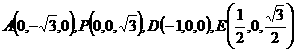 ,
,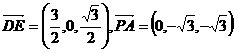 ,
,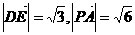 ,
,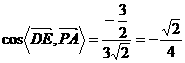 ,
,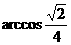 。
。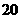 海里的
海里的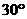 ,相距
,相距 海里
海里 处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往
处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往 )?
)?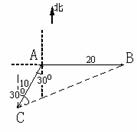 解:
解: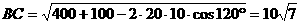
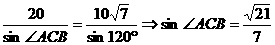
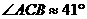
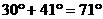 的方向沿直线前往
的方向沿直线前往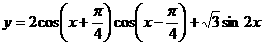 的值域和最小正周期。
的值域和最小正周期。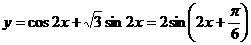 ,
,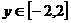 ,
,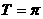 。
。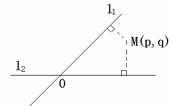 如图,平面中两条直线
如图,平面中两条直线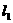 和
和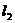 相交于点
相交于点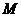 ,若
,若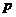 、
、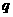 分别是
分别是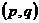 是点
是点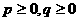 ,给出下列三个命题:
,给出下列三个命题: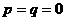 ,则“距离坐标”为
,则“距离坐标”为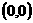 的点有且仅有1个。
的点有且仅有1个。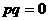 ,且
,且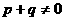 ,则“距离坐标”为
,则“距离坐标”为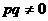 ,则“距离坐标”为
,则“距离坐标”为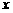 的不等式
的不等式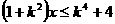 的解集是
的解集是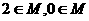 (B)
(B)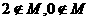 (C)
(C)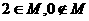 (D)
(D)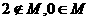
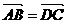 (B)
(B)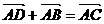
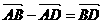 (D)
(D)