0 446849 446857 446863 446867 446873 446875 446879 446885 446887 446893 446899 446903 446905 446909 446915 446917 446923 446927 446929 446933 446935 446939 446941 446943 446944 446945 446947 446948 446949 446951 446953 446957 446959 446963 446965 446969 446975 446977 446983 446987 446989 446993 446999 447005 447007 447013 447017 447019 447025 447029 447035 447043 447348
 ,则复数z的实部为
,则复数z的实部为 .
.
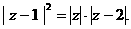
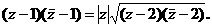
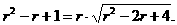
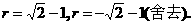
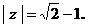
 ∴ CDEF为矩形.
∴ CDEF为矩形. ,
,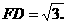

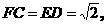
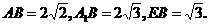

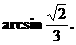
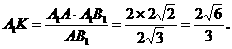

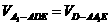
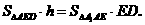
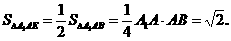
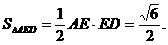
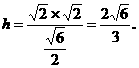
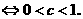
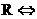 函数y=x+| x-2c | 在R上恒大于1,
函数y=x+| x-2c | 在R上恒大于1,
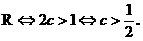
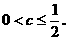
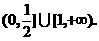
 解法一:设在时刻t(h)台风中心为Q,此时台风侵袭的圆形区域半径为10t+60 (km).
解法一:设在时刻t(h)台风中心为Q,此时台风侵袭的圆形区域半径为10t+60 (km).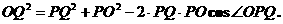
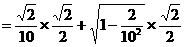
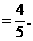
 故
故 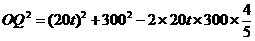

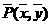 的坐标为
的坐标为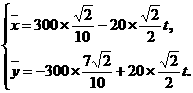

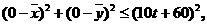
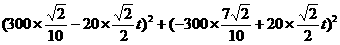
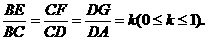
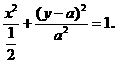
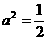 时,点P的轨迹为圆弧,所以不存在符合题意的两点.
时,点P的轨迹为圆弧,所以不存在符合题意的两点. 时,点P的轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长.
时,点P的轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长.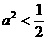 时,点P的椭圆两个焦点
时,点P的椭圆两个焦点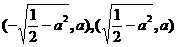 的距离之和为定值
的距离之和为定值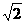
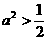 时,点P的椭圆两个焦点
时,点P的椭圆两个焦点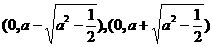 的距离之和为定值2a.
的距离之和为定值2a.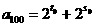 ,只须确定正整数t0,s0
,只须确定正整数t0,s0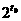 的项构成的子集为
的项构成的子集为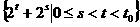 ,
,
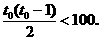
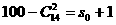 ,由此解得s0=8.
,由此解得s0=8.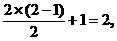
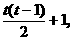 第t行第s个元下标为
第t行第s个元下标为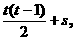 该元等于2t+2t-1.
该元等于2t+2t-1.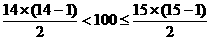 ,所以a100是三角形表第14行的第9个元
,所以a100是三角形表第14行的第9个元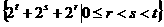 ).
).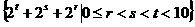 ,
,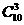 ;
;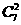 ;
; .
.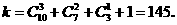
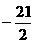 (14)(-1,0) (15)72
(16)①④⑤
(14)(-1,0) (15)72
(16)①④⑤ (Ⅰ)求A1B与平面ABD所成角的大小(结果用反三角函数值表示);
(Ⅰ)求A1B与平面ABD所成角的大小(结果用反三角函数值表示); (20)(本小题满分12分)
(20)(本小题满分12分) 方向300 km的海面P处,并以20 km/h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60 km,并以10 km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?
方向300 km的海面P处,并以20 km/h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60 km,并以10 km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?  (21)(本小题满分14分)
(21)(本小题满分14分) ,P为GE与OF的交点(如图).问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
,P为GE与OF的交点(如图).问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.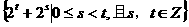 中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,……
中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,……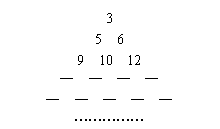
 中所有的数从小到大排列成的数列,已知bk
=1160,求k.
中所有的数从小到大排列成的数列,已知bk
=1160,求k. 展开式中x9的系数是
.
展开式中x9的系数是
.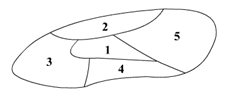 (15)如图,一个地区分为5个行政区域,现给地
图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着色方法共有
种.(以数字作答)
(15)如图,一个地区分为5个行政区域,现给地
图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着色方法共有
种.(以数字作答) (16)下列五个正方体图形中,l是正方体的一条对角线,点M、N、P分别为其所在棱的中点,能得出l⊥面MNP的图形的序号是
.(写出所有符合要求的图形序号)
(16)下列五个正方体图形中,l是正方体的一条对角线,点M、N、P分别为其所在棱的中点,能得出l⊥面MNP的图形的序号是
.(写出所有符合要求的图形序号)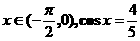 ,则tg 2x=
,则tg 2x= (B)
(B)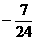 (C)
(C)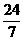 (D)
(D)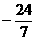
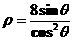 的准线方程是
的准线方程是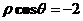 (B)
(B)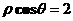 (C)
(C)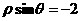 (D)
(D)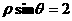
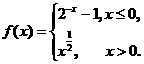 若f(x0)>1,则x0的取值范围是
若f(x0)>1,则x0的取值范围是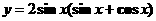 的最大值为
的最大值为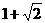 (B)
(B) (C)
(C)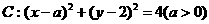 及直线
及直线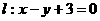 .当直线l被C截得的弦长为
.当直线l被C截得的弦长为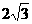 时,则a=
时,则a=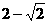 (C)
(C)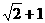
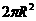 (B)
(B) (C)
(C)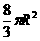 (D)
(D)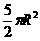
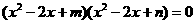 的四个根组成一个首项为
的四个根组成一个首项为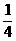 的等差数列,则
的等差数列,则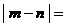
 (C)
(C)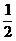 (D)
(D)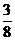
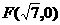 ,直线
,直线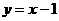 与其相交于M、N两点,MN中点的横坐标为
与其相交于M、N两点,MN中点的横坐标为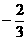 ,则此双曲线的方程是
,则此双曲线的方程是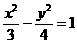 (B)
(B)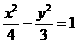 (C)
(C)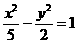 (D)
(D)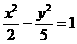
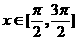 的反函数f-1(x)=
的反函数f-1(x)=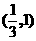 (B)
(B)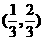 (C)
(C)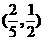 (D)
(D)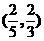
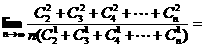
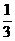 (C)
(C) (D)6
(D)6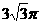 (D)6π
(D)6π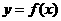 的定义域为
的定义域为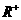 ,对任意
,对任意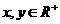 ,有恒等式
,有恒等式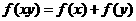 ;且当
;且当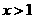 时,
时,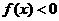 .
.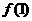 的值;
的值;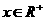 时,恒有
时,恒有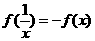 ;
; 上为减函数;
上为减函数; 上的减函数,因而
上的减函数,因而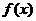 的反函数
的反函数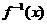 存在,试根据已知恒等式猜想
存在,试根据已知恒等式猜想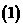 在已知等式中含
在已知等式中含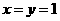 ,得
,得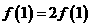 ,
,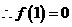 ----------理3分,文5分
----------理3分,文5分 取
取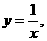 得
得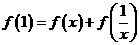
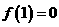 ,
,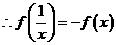 -------------------------------------------------理6分,文10分
-------------------------------------------------理6分,文10分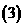 设
设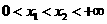 ,并令
,并令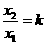 ,则
,则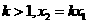
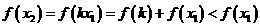
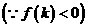
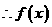 在
在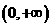 上为减函数----------------------------------------------------理12分,文18分
上为减函数----------------------------------------------------理12分,文18分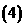 在
在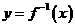 的定义域内,恒有
的定义域内,恒有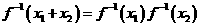 -----------理14分
-----------理14分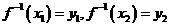 ,则
,则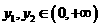
 由题意设
由题意设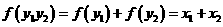
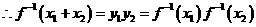 -------------------------------------------------理18分
-------------------------------------------------理18分 (
(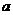 为实常数).
为实常数).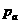 的公共点坐标;
的公共点坐标;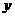 轴为对称轴,且过点
轴为对称轴,且过点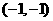 的开口向下的抛物线,使它与某个
的开口向下的抛物线,使它与某个 (
( 为实常数),使它与所有的抛物线
为实常数),使它与所有的抛物线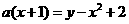
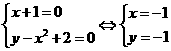
 所有的抛物线
所有的抛物线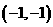 ,即
,即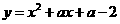
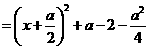 ,即
,即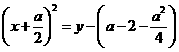
 ,焦点坐标为
,焦点坐标为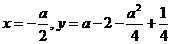
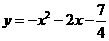 -----------------------------------------------------10分
-----------------------------------------------------10分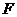 的抛物线可写成
的抛物线可写成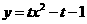
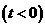 ------------------------------------------------------------------------------------------------------12分
------------------------------------------------------------------------------------------------------12分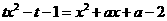 即
即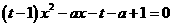
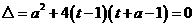
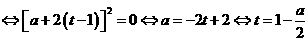 ----14分
----14分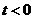
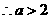 故当
故当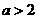 时,存在一条以
时,存在一条以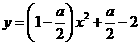 与
与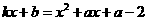 ,
,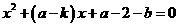 有实根
有实根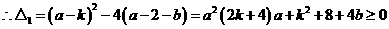
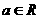 成立。--------------------------------------------------------------------------------------13分
成立。--------------------------------------------------------------------------------------13分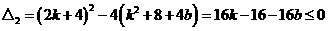
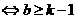
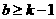 时直线
时直线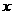 万件与去年促销费
万件与去年促销费 (万元)(
(万元)(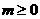 )满足
)满足 .已知2006年生产的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
.已知2006年生产的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).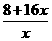 元,故2006年的利润
元,故2006年的利润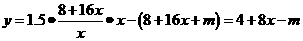 -------------------------------------------4分
-------------------------------------------4分 (万元),
(万元),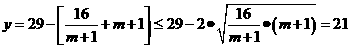 ----------------------------11分
----------------------------11分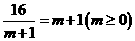 ,即
,即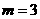 (万元)时成立。
(万元)时成立。