海淀2007高三数学查漏补缺题
07年高考数学北京卷应该是在06年北京卷成功的基础上,稳定的发展,复习中要对各区题目(尤其东城、西城、海淀)文科理科中重点板块不仅要明确知识点,而且还要掌握结构特点,要用联系的思想看知识间的综合,用运动的观点看能力的要求. 高考数学试题是以思维能力考查为主体的,试题展现数学关系常常选取不同展示形式(图表、图象、曲线图、表格、符号、等等)之一,同学们要善于利用数学信息的多种表述分析问题,联系已有知识方法,提高分析问题、解决问题能力.
一、函数与导数
1.〖理科〗 已知函数f (x)=6lnx―ax2―8x+b (a,b为常数),且x =3为f (x)的一个极值点.
(Ⅰ) 求a;
(Ⅱ) 求函数f (x)的单调区间;
(Ⅲ) 若y = f (x)的图象与x轴正半轴有且只有3个交点,求实数b的取值范围.
解: (Ⅰ) ∵ f ′ (x) = ―2ax―8, ∴ f ′ (3) =2―
―2ax―8, ∴ f ′ (3) =2―
(Ⅱ) 函数f (x)的定义域为(0,+∞).
由(Ⅰ) 知f (x) =6lnx+x2―8x+b.
∴
f ′ (x) = +2x―8=
+2x―8= .
.
由f ′ (x)>0可得x>3或x<1,由f ′ (x)<0可得1<x<3.
∴函数f (x)的单调递增区间为(0,1)和(3,+∞),单调递减区间为(1,3).
(注:单调区间应分开写,不能用“È”连接)
(Ⅲ) 由(Ⅱ)可知函数f (x)在(0,1)单调递增,在(1,3)单调递减,在(3,+∞)单调递增.
且当x=1或x=3时,f ′ (x)=0.
∴ f (x)的极大值为f (1)=6ln1+1―8+b=b―7,
f (x)的极小值为f (3)=6ln3+9―24+b=6ln3+b―15.
∵当x充分接近0时,f (x)<0,当x充分大时,f (x)>0,
∴要使f (x)的图象与x轴正半轴有且仅有三个不同的交点,只需

则7<b<15―6ln3
2.〖理科、文科〗设函数 ,其图象在点
,其图象在点 处的切线的斜率分别为
处的切线的斜率分别为 .
.
(Ⅰ)求证: ;
;
(Ⅱ)若函数 的递增区间为
的递增区间为 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)若当 时(k是与
时(k是与 无关的常数),恒有
无关的常数),恒有 ,试求k的最小值.
,试求k的最小值.
(Ⅰ)证明: ,由题意及导数的几何意义得
,由题意及导数的几何意义得
 ,
, (1)
(1)
 ,
(2)
,
(2)
又 ,可得
,可得 ,即
,即 ,故
,故
由(1)得 ,代入
,代入 ,再由
,再由 ,得
,得
 ,
(3)
,
(3)
将 代入(2)得
代入(2)得 ,即方程
,即方程 有实根.
有实根.
故其判别式 得
得
 ,或
,或 , (4)
, (4)
由(3),(4)得 ;
;
(Ⅱ)解:由 的判别式
的判别式 ,
,
知方程 有两个不等实根,设为
有两个不等实根,设为 ,
,
又由 知,
知, 为方程(
为方程( )的一个实根,则由根与系数的关系得
)的一个实根,则由根与系数的关系得
 ,
,
当 或
或 时,
时, ,当
,当 时,
时, ,
,
故函数 的递增区间为
的递增区间为 ,由题设知
,由题设知 ,
,
因此 ,由(Ⅰ)知
,由(Ⅰ)知 得
得
 的取值范围为
的取值范围为 ;
;
(Ⅲ)解:由 ,即
,即 ,即
,即 ,
,
因为 ,则
,则 ,整理得
,整理得 ,
,
设 ,可以看作是关于
,可以看作是关于 的一次函数,
的一次函数,
由题意 对于
对于 恒成立,
恒成立,
故 即
即 得
得 或
或 ,
,
由题意, ,
,
故 ,因此
,因此 的最小值为
的最小值为 .
.
二、数列
3.对于数列{an}, {cn}数列,其中cn=an+1― an (nÎN*).
(Ⅰ) 若数列{an}的通项公式 (nÎN*),求{cn}的通项公式;
(nÎN*),求{cn}的通项公式;
(Ⅱ) 若数列{an}的首项是1,且满足cn― an=2n.
(1) 求证:数列 为等差数列;
为等差数列;
(2) (理) 若 (nÎN*),求证:
(nÎN*),求证: .
.
(文) 求数列{an}的前n项和Sn.
证明:(Ⅰ)依题意cn=an+1― an,
∴ cn= .
.
(Ⅱ)(1)由cn― an=2n得an+1― an― an=2n,即an+1=2an+2n.
∴ ,即
,即 .
.
∵a1=1, ,∴
,∴ 是以
是以 为首项、
为首项、 为公差的等差数列.
为公差的等差数列.
(2)(理)由(1)知an=n?2n-1.
∴  .
.
∴  .
∴
.
∴ 
= .
.
=
(文)由(1)得an= =n?2n-1,
=n?2n-1,
∴ Sn = a1+a2+…+an=1?20+2?21+…+n?2n-1, ①
∴ 2Sn=1?21+2?22+…+n?2n. ②
①―②得:― Sn=1+2+22+…+2n-1― n?2n = ― n?2n,
― n?2n,
∴ Sn= n?2n― 2n+1=(n― 1)?2n +1.
4.〖理科、文科〗 设数列 的各项都是正数,记Sn为数列
的各项都是正数,记Sn为数列 的前n项和,且对任意n∈N+,都有
的前n项和,且对任意n∈N+,都有 .
.
(Ⅰ)求证: =2Sn-an;
=2Sn-an;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)若 (
( 为非零常数,n∈N+),问是否存在整数
为非零常数,n∈N+),问是否存在整数 ,使得对任意 n∈N+,都有bn+1>bn.
,使得对任意 n∈N+,都有bn+1>bn.
(Ⅰ)证明:在已知式中,当n=1时,
∵a1>0 ∴a1=1……………………………………1分
当n≥2时, ①
①
 ②
②
①-②得, …………………………3分
…………………………3分
∵an>0 ∴ =
=
即 =2Sn-an ∵a1=1适合上式
=2Sn-an ∵a1=1适合上式
∴ =2Sn-an(n∈N+)……………………5分
=2Sn-an(n∈N+)……………………5分
(Ⅱ)解:由(1)知 =2Sn-an(n∈N+) ③
=2Sn-an(n∈N+) ③
当n≥2时,  =2Sn-1-an-1
④
=2Sn-1-an-1
④
③-④得 -
- =2(Sn-Sn-1)-an+an-1=2an-an+ an-1= an+
an-1
=2(Sn-Sn-1)-an+an-1=2an-an+ an-1= an+
an-1
∵an+an-1>0 ∴an-an-1=1……………………8分
∴数列{an}是等差数列,首项为1,公差为1,可得an=n………………9分
(Ⅲ)解:∵
欲使
即 成立 ⑤……………………11分
成立 ⑤……………………11分
当n=2k-1,k=1,2,3,…时,⑤式即为 ⑥
⑥
依题意,⑥式对k=1,2,3…都成立,∴λ<1………………12分
当n=2k,k=1,2,3,…时,⑤式即为 ⑦
⑦
依题意,⑦式对k=1,2,3,…都成立,
∴ ……………………13分
……………………13分
∴
∴存在整数λ=-1,使得对任意n∈N+,都有 >
>
三、立体几何
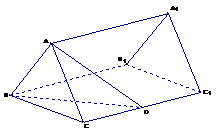 5. 〖理科、文科〗 如图,已知正三棱柱
5. 〖理科、文科〗 如图,已知正三棱柱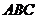 ―
―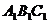 的底面边长是
的底面边长是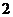 ,
,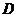 是侧棱
是侧棱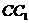 的中点,直线
的中点,直线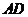 与侧面
与侧面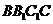 所成的角为
所成的角为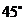 .
.
(Ⅰ)求此正三棱柱的侧棱长;
(Ⅱ) 求二面角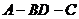 的大小;
的大小;
(Ⅲ)求点 到平面
到平面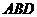 的距离.
的距离.
 (Ⅰ)证明:设正三棱柱
(Ⅰ)证明:设正三棱柱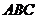 ―
―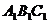 的侧棱长为
的侧棱长为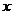 .取
.取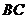 中点
中点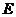 ,连
,连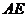 .
.
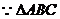 是正三角形,
是正三角形,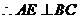 .
.
又底面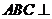 侧面
侧面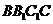 ,且交线为
,且交线为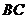 .
.
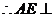 侧面
侧面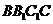 .
.
连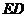 ,则直线
,则直线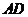 与侧面
与侧面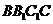 所成的角为
所成的角为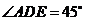 .
.
在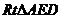 中,
中, ,解得
,解得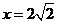 .
.
 此正三棱柱的侧棱长为
此正三棱柱的侧棱长为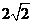 .
.
注:也可用向量法求侧棱长.
(Ⅱ)解:解法1:过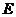 作
作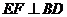 于
于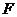 ,连
,连 ,
,
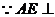 侧面
侧面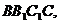

 .
.
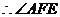 为二面角
为二面角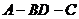 的平面角.
的平面角.
在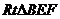 中,
中,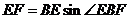 ,又
,又
 ,
, 
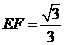 .
.
又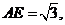
 在
在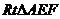 中,
中,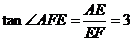 .
.
故二面角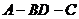 的大小为
的大小为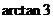 .
.
解法2:(向量法,见后)
(Ⅲ)解:解法1:由(Ⅱ)可知,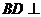 平面
平面 ,
, 平面
平面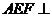 平面
平面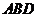 ,且交线为
,且交线为 ,
, 过
过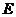 作
作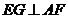 于
于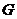 ,则
,则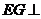 平面
平面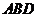 .
.
在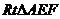 中,
中,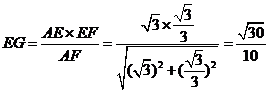 .
.
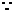
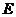 为
为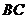 中点,
中点, 点
点 到平面
到平面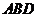 的距离为
的距离为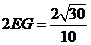 .
.
解法2: (思路)等体积变换:由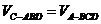 可求.
可求.
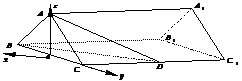 解法3: (向量法,见后)
解法3: (向量法,见后)
题(Ⅱ)、(Ⅲ)的向量解法:
(Ⅱ)解法2:如图,建立空间直角坐标系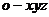 .
.
则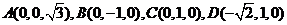 .
.
设
 为平面
为平面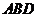 的法向量.
的法向量.
由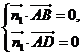 得
得
 .
.
 取
取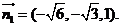
又平面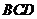 的一个法向量
的一个法向量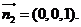

 .
.
结合图形可知,二面角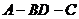 的大小为
的大小为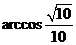 .
.
(Ⅲ)解法3:由(Ⅱ)解法2,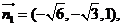
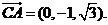
 点
点 到平面
到平面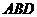 的距离
的距离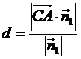
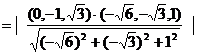 =
=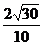 .
.
注:若为了看图方便,也可以把图调整后,标好字母证明之.
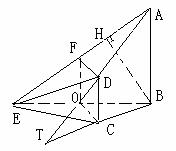
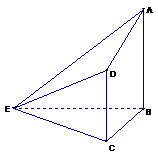 6. 〖理科、文科〗如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD= 2, ∠BCE=1200.
6. 〖理科、文科〗如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD= 2, ∠BCE=1200.
(Ⅰ)求证:平面ADE⊥平面ABE ;
(Ⅱ)求点C到平面ADE的距离.
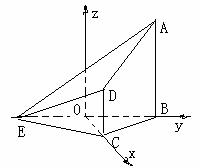 解法1:取BE的中点O,连OC.
解法1:取BE的中点O,连OC.
∵BC=CE, ∴OC⊥BE.又AB⊥平面BCE.
以O为原点建立空间直角坐标系O-xyz如图,
则由已知条件有: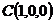 ,
,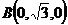 ,
,
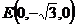
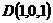 ,
,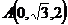
设平面ADE的法向量为n=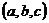 ,
,
则由n?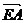
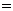
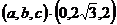
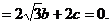
及n?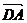
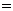
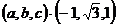
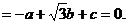
可取n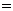
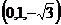
又AB⊥平面BCE. ∴AB⊥OC.OC⊥平面ABE
∴平面ABE的法向量可取为m=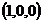 .
.
∵n?m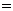
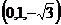 ?
?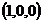 =0,
=0,
∴n⊥m∴平面ADE⊥平面ABE.
(Ⅱ)点C到平面ADE的距离为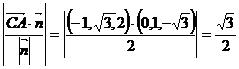
解法2:取BE的中点O,AE的中点F,连OC,OF,DF.则
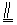
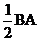
 ∵AB⊥平面BCE,CD⊥平面BCE, AB=2CD
∵AB⊥平面BCE,CD⊥平面BCE, AB=2CD
∴CD 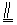
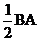 ,
,
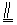 CD∴
CD∴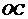 ∥ FD
∥ FD
∵BC=CE, ∴OC⊥BE.又AB⊥平面BCE.
∴OC⊥平面ABE. ∴FD⊥平面ABE.
从而平面ADE⊥平面ABE.
(Ⅱ)∵CD 
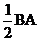 ,延长AD, BC交于T
,延长AD, BC交于T
则C为BT的中点.
点C到平面ADE的距离等于点B到平面ADE的距离的 .
.
过B作BH⊥AE,垂足为H.∵平面ADE.⊥平面ABE.∴BH⊥平面BDE.
由已知有AB⊥BE.
BE=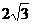 ,AB= 2, ∴BH=
,AB= 2, ∴BH=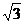 ,
,
从而点C到平面ADE的距离为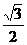
或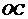 ∥ FD, 点C到平面ADE的距离等于点O到平面ADE的距离为
∥ FD, 点C到平面ADE的距离等于点O到平面ADE的距离为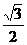 .
.
或取A B的中点M.易证 ∥ DA.点C到平面ADE的距离等于点M到平面ADE的距离为
∥ DA.点C到平面ADE的距离等于点M到平面ADE的距离为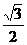 .
.
四、三角函数
7.〖理科、文科〗已知三点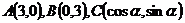 ,其中
,其中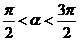 .
.
(Ⅰ)若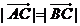 ,求角
,求角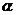 的值;
的值;
(Ⅱ)若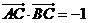 ,求
,求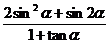 的值.
的值.
解:(Ⅰ) 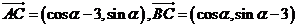 .
.
∵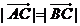 ,∴
,∴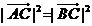 ,即
,即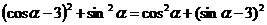 ,
,
化简得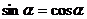 ,∴
,∴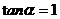 .
.
∵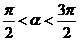 ,∴
,∴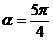 .
.
(Ⅱ) 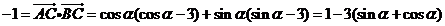 ,
,
 ,
,
∴
8.〖理科、文科〗已知: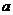 为实数,函数
为实数,函数
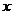 ∈R.
∈R.
(Ⅰ)设 求
求 的取值范围;
的取值范围;
(Ⅱ)当 的最大值是3时,求
的最大值是3时,求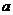 的值.
的值.
解:
 的取值范围是
的取值范围是


令
(1)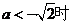
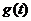 的最大值为
的最大值为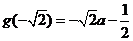
依题意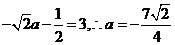 (满足
(满足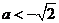 )
)
(2)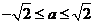 时
时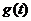 的最大值为
的最大值为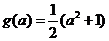
依题意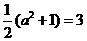 ,所以,
,所以,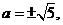 不满足题意.
不满足题意.
(3)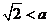 时,
时, 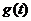 的最大值为
的最大值为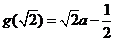
依题意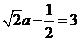 ,
,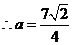 ,满足
,满足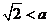 .
.
由以上知: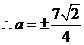 .
.
五、概率
9. 〖理科〗某保险公司的统计表明,新保险的汽车司机中可划分为两类:第一类人易出事故,其在一年内出事故的概率为0.4,第二类人为谨慎的人,其在一年内出事故的概率为0.2.假定在新投保的3人中有一人是第一类人,有两人是第二类人.一年内这3人中出现事故的人数为记为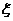 .(设这三人出事故与否互不影响)
.(设这三人出事故与否互不影响)
(Ⅰ)求三人都不出事故的概率;
(Ⅱ)求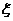 的分布列及数学期望.
的分布列及数学期望.
解:(Ⅰ)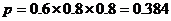
(Ⅱ)
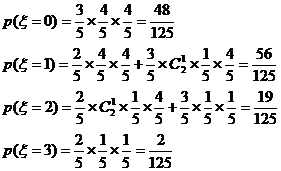
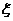
0
1
2
3
p
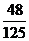
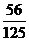
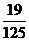


10. 〖理科、文科〗三名学生进行投篮测试,投中两次就停止投篮记为过关,每人最多可投4次.已知每位同学每次投中的概率均为 ,且各次投篮投中与否互不影响.
,且各次投篮投中与否互不影响.
(Ⅰ)求每位同学过关的概率;
(Ⅱ)求恰有两位同学过关的概率;
(Ⅲ)求至少有一位同学过关的概率.
解:(Ⅰ)设每位同学过关的概率记为p
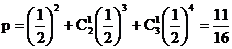
(Ⅱ) 设恰有两位同学过关的概率为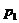
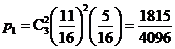
(Ⅲ)设至少有一位同学过关的概率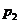
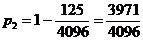
六、不等式
11、〖理〗已知关于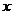 的不等式
的不等式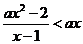 的解集为
的解集为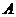 ,且
,且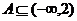 .求
.求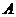
解:易知对任意的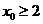 ,均有
,均有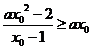
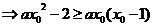
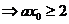
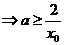
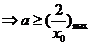
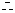
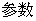
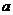 的取值范围是
的取值范围是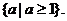
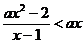
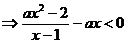
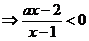


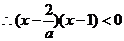
当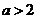 时,有
时,有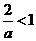 ,故
,故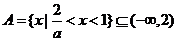 ,
,
当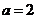 时,
时,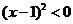 ,故
,故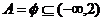 ,
,
当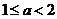 时,有
时,有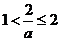 ,故
,故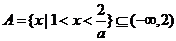 ,
,
因此,当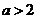 时,
时, ,
,
当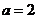 时,
时,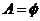 ,
,
当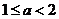 时,
时,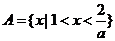 .
.
12、〖理科、文科〗若实数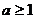 ,解关于
,解关于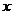 的不等式
的不等式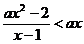 .
.
解: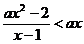
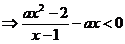
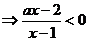


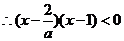
当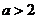 时,有
时,有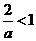 ,故不等式的解集为
,故不等式的解集为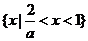 ,
,
当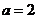 时,不等式转化为
时,不等式转化为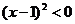 ,故不等式的解集为
,故不等式的解集为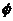 ,
,
当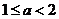 时,有
时,有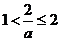 ,故不等式的解集为
,故不等式的解集为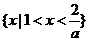 .
.
七、解析几何
13. 〖理科、文科〗已知两定点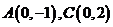 ,动点M满足
,动点M满足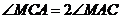 .
.
(Ⅰ)求动点M的轨迹Q的方程;
(Ⅱ)设曲线Q与y轴的交点为B,点E、F是曲线Q上两个不同的动点,且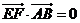 ,直线AE与BF交于点
,直线AE与BF交于点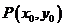 ,求证:
,求证: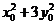 为定值;
为定值;
(Ⅲ) 〖理科〗在第(Ⅱ)问的条件下,求证:过点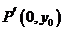 和点E的直线是曲线Q的一条切线.
和点E的直线是曲线Q的一条切线.
(Ⅳ)在第(Ⅱ)问的条件下,试问是否存在点E使得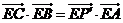 (或
(或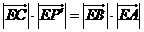 ),若存在,求出此时点E的坐标;若不存在,说明理由.
),若存在,求出此时点E的坐标;若不存在,说明理由.
解:(Ⅰ)设动点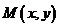 ,因为
,因为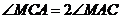
所以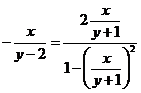 或
或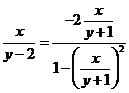
化简得: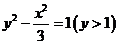
(Ⅱ)由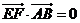 可设点
可设点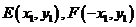 则由A、P、E三点共线可得
则由A、P、E三点共线可得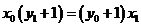 ,同理可得:
,同理可得: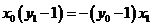 ,两式相乘得:
,两式相乘得: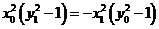 ,又因为
,又因为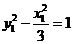 ,所以
,所以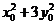 =3
=3
(Ⅲ)点E处曲线Q的切线的斜率为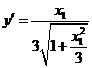 ,则切线方程为
,则切线方程为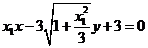 ,AE、BF的方程为
,AE、BF的方程为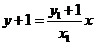 ,
,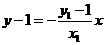 ,则
,则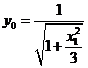 ,所以
,所以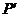 在上述切线上,即过点
在上述切线上,即过点 和点E的直线是曲线Q的一条切线.
和点E的直线是曲线Q的一条切线.
(Ⅳ) 先证: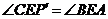
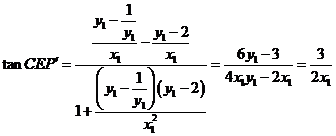 (其中用到
(其中用到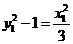 代换)
代换)
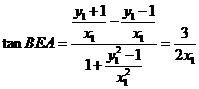
由此可得: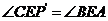 .
.
要使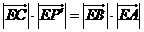 ,则只需
,则只需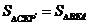 ,即
,即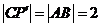 .而
.而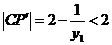 ,因此不存在点E使得
,因此不存在点E使得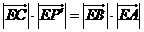 成立.
成立.
另解:同前可得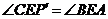 ,要使
,要使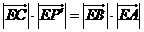 ,则只需
,则只需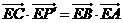 ,即
,即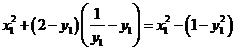 ,化简得
,化简得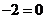 ,显然不成立.
,显然不成立.
14〖理科、文科〗如图,已知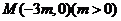 ,N、P两点分别在
,N、P两点分别在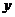 轴和
轴和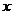 轴上运动,并且满足
轴上运动,并且满足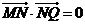 ,
,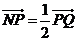
(Ⅰ)求动点Q的轨迹方程;
(Ⅱ)若正方形ABCD的三个顶点A、B、C在点Q的轨迹上,求正方形ABCD面积的最小值.
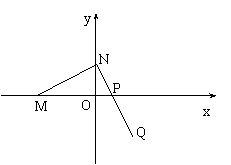 解(Ⅰ)
解(Ⅰ)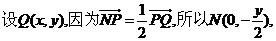
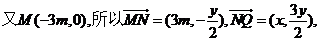
由已知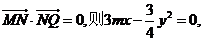

(Ⅱ)如图,不妨设正方形在抛物线上的三个顶点中A、B在x轴的下方(包括x轴),记A、B、C的坐标分别为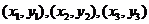 ,其中
,其中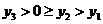
并设直线AB的斜率为k(k<0)
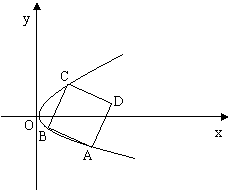 则有
则有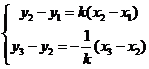 ……①
……①
又因为A、B、C在抛物线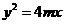 上,故有
上,故有
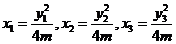 代入①式得
代入①式得
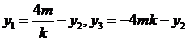 ……②
……②
∵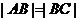
即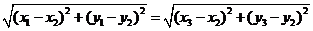
∴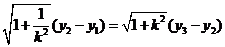
∴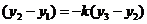 将②代入可得:
将②代入可得:
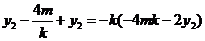
即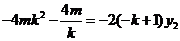 ,
,
得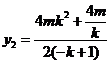
正方形的边长为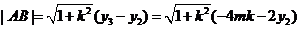
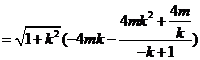
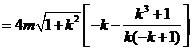
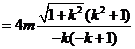
易知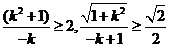
所以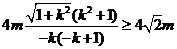
所以正方形ABCD面积的最小值为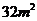 .
.
祝同学们考试顺利!