摘要: [理科.文科]如图.在四棱锥E-ABCD中,AB⊥平面BCE.CD⊥平面BCE.AB=BC=CE=2CD= 2, ∠BCE=1200.(Ⅰ)求证:平面ADE⊥平面ABE ,(Ⅱ)求点C到平面ADE的距离.
网址:http://m.1010jiajiao.com/timu_id_34583[举报]
(理科)如图的多面体是底面为平行四边形的直四棱柱ABCD-A1B1C1D1,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.

(Ⅰ)求证:BD⊥平面ADG;
(Ⅱ)求平面AEFG与平面ABCD所成锐二面角的余弦值.
(文科)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
(Ⅰ)求证:AF⊥平面CBF;
(Ⅱ)设FC的中点为M,求证:OM∥平面DAF.
 查看习题详情和答案>>
查看习题详情和答案>>

(Ⅰ)求证:BD⊥平面ADG;
(Ⅱ)求平面AEFG与平面ABCD所成锐二面角的余弦值.
(文科)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
(Ⅰ)求证:AF⊥平面CBF;
(Ⅱ)设FC的中点为M,求证:OM∥平面DAF.
 查看习题详情和答案>>
查看习题详情和答案>>
(理科)如图, 是边长为
是边长为 的正方形,
的正方形, 和
和 都与平面
都与平面 垂直,且
垂直,且
 ,设平面
,设平面 与平面
与平面 所成二面角为
所成二面角为 ,则
,则 ▲
▲
(文科)如图,二面角 的大小是60°,线段
的大小是60°,线段 .
. ,
,

 与
与 所成的角为30°.则
所成的角为30°.则 与平面
与平面 所成的角的正弦值是▲
所成的角的正弦值是▲
查看习题详情和答案>>




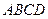 是边长为
是边长为 的正方形,
的正方形,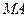 和
和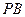 都与平面
都与平面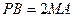
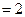 ,设平面
,设平面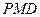 与平面
与平面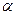 ,则
,则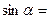 ▲
▲ 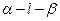 的大小是60°,线段
的大小是60°,线段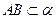 .
.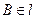 ,
,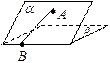
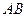 与
与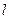 所成的角为30°.则
所成的角为30°.则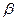 所成的角的正弦值是▲
所成的角的正弦值是▲