摘要:连.则直线与侧面所成的角为.
网址:http://m.1010jiajiao.com/timu_id_34557[举报]
如图,在正四棱锥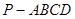 中,
中,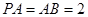 .
.
(1)求该正四棱锥的体积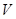 ;
;
(2)设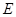 为侧棱
为侧棱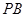 的中点,求异面直线
的中点,求异面直线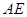 与
与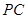
所成角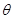 的大小.
的大小.
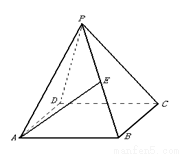
【解析】第一问利用设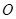 为底面正方形
为底面正方形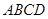 中心,则
中心,则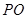 为该正四棱锥的高由已知,可求得
为该正四棱锥的高由已知,可求得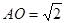 ,
,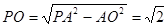
所以,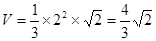
第二问设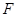 为
为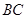 中点,连结
中点,连结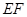 、
、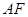 ,
,
可求得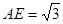 ,
,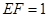 ,
,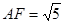 ,
,
在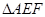 中,由余弦定理,得
中,由余弦定理,得
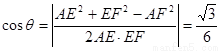 .
.
所以,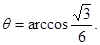
查看习题详情和答案>>
13、下列结论正确的是
①各个面都是三角形的几何体是三棱锥;
②以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥;
③棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是正六棱锥;
④圆锥的顶点与底面圆周上的任意一点的连线都是母线.
查看习题详情和答案>>
④
①各个面都是三角形的几何体是三棱锥;
②以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥;
③棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是正六棱锥;
④圆锥的顶点与底面圆周上的任意一点的连线都是母线.
下列结论正确的是______
①各个面都是三角形的几何体是三棱锥;
②以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥;
③棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是正六棱锥;
④圆锥的顶点与底面圆周上的任意一点的连线都是母线.
查看习题详情和答案>>
①各个面都是三角形的几何体是三棱锥;
②以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥;
③棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是正六棱锥;
④圆锥的顶点与底面圆周上的任意一点的连线都是母线.