6、解:(1)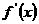 =
=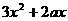
依题意得k=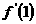 =3+2a=-3, ∴a=-3
=3+2a=-3, ∴a=-3
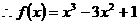 ,把B(1,b)代入得b=
,把B(1,b)代入得b=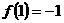
∴a=-3,b=-1
(2)令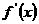 =3x2-6x=0得x=0或x=2
=3x2-6x=0得x=0或x=2
∵f(0)=1,f(2)=23-3×22+1=-3
f(-1)=-3,f(4)=17
∴x∈[-1,4],-3≤f(x)≤17
要使f(x)≤A-1987对于x∈[-1,4]恒成立,则f(x)的最大值17≤A-1987
∴A≥2004。
(1)
已知g(x)=-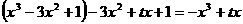
∴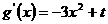
∵0<x≤1,∴-3≤-3x2<0,
①
当t>3时,t-3x2>0,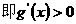
∴g(x)在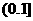 上为增函数,
上为增函数,
g(x)的最大值g(1)=t-1=1,得t=2(不合题意,舍去)
②
当0≤t≤3时, 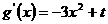
令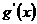 =0,得x=
=0,得x=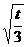
列表如下:
|
x |
(0, 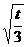 ) ) |
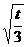 |
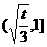 |
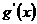 |
+ |
0 |
- |
|
g(x) |
↗ |
极大值 |
↘ |
g(x)在x=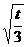 处取最大值-
处取最大值-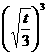 +t
+t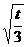 =1
=1
∴t=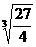 =
=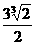 <
<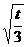 3
3
∴x=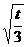 <1
<1
③当t<0时,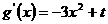 <0,∴g(x)在
<0,∴g(x)在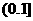 上为减函数,
上为减函数,
∴g(x)在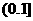 上为增函数,
上为增函数,
∴存在一个a=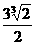 ,使g(x)在
,使g(x)在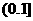 上有最大值1。
上有最大值1。
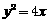 的焦点F的直线
的焦点F的直线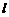 与该抛物线交于
与该抛物线交于 、
、 两点. (12分)
两点. (12分) 的中点为
的中点为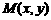 ,直线的斜率为
,直线的斜率为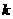 ,试求点
,试求点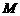 的坐标,并求点
的坐标,并求点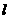 的斜率
的斜率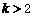 ,且点
,且点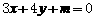 的距离为
的距离为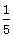 ,试确定
,试确定 的取值范围.
的取值范围.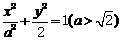 。
。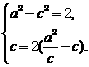 解得
解得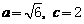
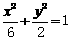 ,离心率
,离心率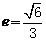 。
。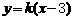 。由方程组
。由方程组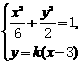
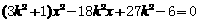 ,依题意
,依题意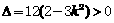 ,得
,得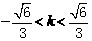 。
。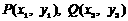 ,则
,则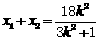 , ①
, ① 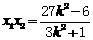 。 ②
。 ②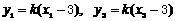 。于是
。于是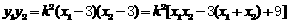 。 ③
。 ③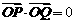 ,∴
,∴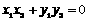 。 ④
。 ④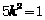 ,从而
,从而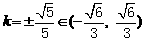 。
。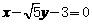 或
或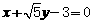
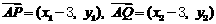 。由已知得方程组
。由已知得方程组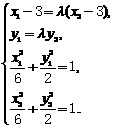
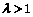 ,解得
,解得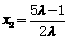
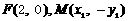 ,故
,故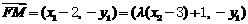
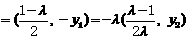 。
。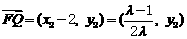 ,所以
,所以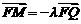 。
。 (2k≦x≦2k+2,
k∈Z) ②略 ⑶方程在[1,4]上有4个实根
(2k≦x≦2k+2,
k∈Z) ②略 ⑶方程在[1,4]上有4个实根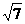
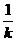 x+1
x+1 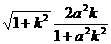 ,同理|AB|=
,同理|AB|=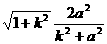

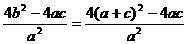
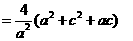
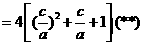
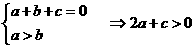 ,而a>0,∴
,而a>0,∴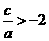
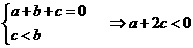 ,∴
,∴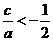
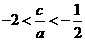
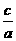 )2+
)2+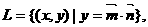 其中
其中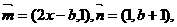 点列
点列 在
在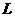 中,
中,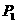 为
为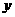 轴的交点,等差数列
轴的交点,等差数列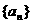 的公差为1,
的公差为1,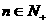 。
。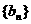 的通项公式;
的通项公式;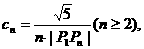 求
求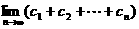 ;
;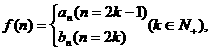 是否存在
是否存在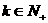 使得
使得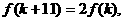 若存在,求出
若存在,求出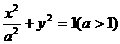 ,直线l过点A(-a,0)和点B(a,ta)
,直线l过点A(-a,0)和点B(a,ta) (2)若t∈[1,2],a为定值,求S的最大值.
(2)若t∈[1,2],a为定值,求S的最大值.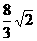 ,MN的中点到Y轴的距离为
,MN的中点到Y轴的距离为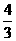 ,求椭圆的方程。
,求椭圆的方程。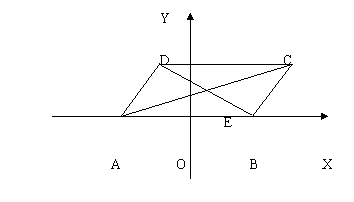
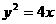 的准线与
的准线与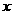 轴交于
轴交于 点,过
点,过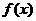 是定义在R上的偶函数.当X
是定义在R上的偶函数.当X 0时,
0时, 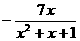 .
. 的单调性,并证明你的结论.
的单调性,并证明你的结论.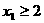 且
且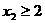 ,证明:|
,证明:|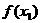 -
-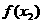 |<2.
|<2.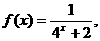
 为定值;
为定值;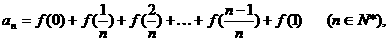 求数列
求数列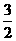 ,BC=
,BC=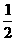 .椭圆C以A、B为焦点且经过点D.
.椭圆C以A、B为焦点且经过点D.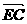

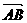 ,问是否存在不平行AB的直线l与椭圆C交于M、N两点且
,问是否存在不平行AB的直线l与椭圆C交于M、N两点且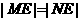 ,若存在,求出直线l与AB夹角的范围,若不存在,说明理由.
,若存在,求出直线l与AB夹角的范围,若不存在,说明理由.