摘要:21.经过抛物线的焦点F的直线与该抛物线交于.两点. (1)若线段的中点为,直线的斜率为,试求点的坐标,并求点的轨迹方程 (2)若直线的斜率,且点到直线的距离为,试确定的取值范围. 1(1)解:由题意.可设椭圆的方程为. 由已知得解得 所以椭圆的方程为.离心率. . 设直线PQ的方程为.由方程组 得.依题意.得. 设.则. ① . ② 由直线PQ的方程得.于是 . ③ ∵.∴. ④ 由①②③④得.从而. 所以直线PQ的方程为或 证明:.由已知得方程组 注意.解得 因.故 . 而.所以. 2 ①f(x)= ②略 ⑶方程在[1.4]上有4个实根 3 ①x2=4y ②x1x2=-4 ⑶P SMIN= 4 .解:因a>1.不防设短轴一端点为B(0.1) 设BC∶y=kx+1(k>0) 则AB∶y=-x+1 把BC方程代入椭圆. 是(1+a2k2)x2+2a2kx=0 ∴|BC|=.同理|AB|= 由|AB|=|BC|.得k3-a2k2+ka2-1=0 (k-1)[k2+(1-a2)k+1]=0 ∴k=1或k2+(1-a2)k+1=0 当k2+(1-a2)k+1=0时.Δ=(a2-1)2-4 由Δ<0.得1<a< 由Δ=0.得a=.此时.k=1 故.由Δ≤0.即1<a≤时有一解 由Δ>0即a>时有三解 5 解:依题意.知a.b≠0 ∵a>b>c且a+b+c=0 ∴a>0且c<0 (Ⅰ)令f(x)=g(x). 得ax2+2bx+c=0.(*) Δ=4(b2-ac) ∵a>0.c<0.∴ac<0.∴Δ>0 ∴f(x).g(x)相交于相异两点 (Ⅱ)设x1.x2为交点A.B之横坐标 则|A1B1|2=|x1-x2|2.由方程(*).知 |A1B1|2= ∵.而a>0.∴ ∵.∴ ∴ ∴4[()2++1]∈ ∴|A1B1|∈(.2)
网址:http://m.1010jiajiao.com/timu3_id_500029[举报]
 已知抛物线的顶点在坐标原点,对称轴为x轴,焦点F在直线m:y=
已知抛物线的顶点在坐标原点,对称轴为x轴,焦点F在直线m:y=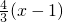 上,直线m与抛物线相交于A,B两点,P为抛物线上一动点(不同于A,B),直线PA,PB分别交该抛物线的准线l于点M,N.
上,直线m与抛物线相交于A,B两点,P为抛物线上一动点(不同于A,B),直线PA,PB分别交该抛物线的准线l于点M,N.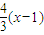 上,直线m与抛物线相交于A,B两点,P为抛物线上一动点(不同于A,B),直线PA,PB分别交该抛物线的准线l于点M,N.
上,直线m与抛物线相交于A,B两点,P为抛物线上一动点(不同于A,B),直线PA,PB分别交该抛物线的准线l于点M,N.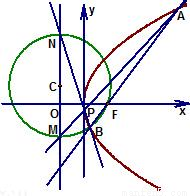
 已知抛物线y2=8x与椭圆
已知抛物线y2=8x与椭圆