0 49656 49664 49670 49674 49680 49682 49686 49692 49694 49700 49706 49710 49712 49716 49722 49724 49730 49734 49736 49740 49742 49746 49748 49750 49751 49752 49754 49755 49756 49758 49760 49764 49766 49770 49772 49776 49782 49784 49790 49794 49796 49800 49806 49812 49814 49820 49824 49826 49832 49836 49842 49850 447348
 已知
已知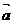 、
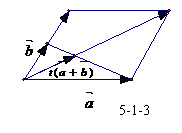
、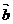 是两个不共线的向量,若它们起点相同,
是两个不共线的向量,若它们起点相同,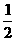
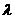 使:t(
使:t(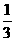

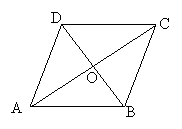
 ABCD的两条对角线AC与BD交于E,O是任意一点,
ABCD的两条对角线AC与BD交于E,O是任意一点,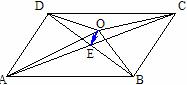 求证:
求证: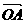 +
+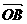 +
+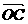 +
+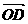 =4
=4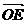
 量的定义可得。
量的定义可得。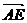 =
=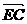 =-
=-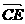 ,
,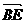 =
=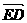 =-
=-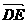

 解析: =+ = -3a+2b,
解析: =+ = -3a+2b,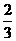 b =,
b =,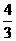 b.
b.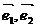 是不共线的向量,已知向量
是不共线的向量,已知向量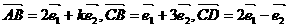 ,若A,B,D三点共线,求k的值
,若A,B,D三点共线,求k的值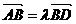
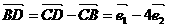 , 使
, 使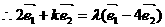
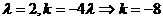
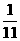 a-
a- b④
b④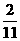 b
b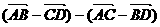
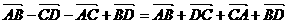
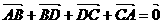
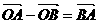 )
)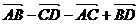
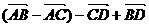
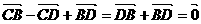
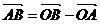 )
)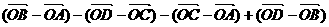
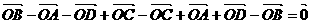
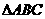 所在的平面上有一点
所在的平面上有一点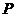 ,满足
,满足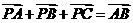 ,则
,则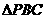 与
与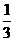 B.
B.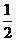 C.
C.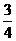
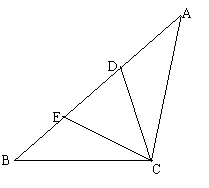
 [解题思路]: 本题中的已知向量都集中体现在三角形中.为此,可充分利用向量加减法的三角形法则实施求解.
[解题思路]: 本题中的已知向量都集中体现在三角形中.为此,可充分利用向量加减法的三角形法则实施求解.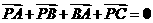 ,
,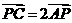 ,所以点
,所以点 边上的第二个三等分点,如图所示.
边上的第二个三等分点,如图所示.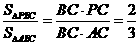 .
.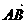 与
与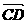 是共线向量,则A、B、C、D四点必在一直线上;
是共线向量,则A、B、C、D四点必在一直线上; 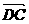
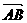 、
、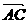 在同一直线上.
在同一直线上.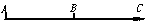 ④、⑤正确.⑥不正确.如图
④、⑤正确.⑥不正确.如图 共线,虽起点不同,但其终点却相同.
共线,虽起点不同,但其终点却相同. a=λb,只有b≠0才是正确的.而当b=0时,a∥b是a=λb的必要不充分条件.
a=λb,只有b≠0才是正确的.而当b=0时,a∥b是a=λb的必要不充分条件.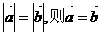
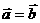 ,
,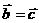 ,则
,则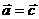 ;
;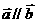 ,
,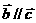 ,则
,则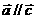 (8)若四边形ABCD是平行四边形,则
(8)若四边形ABCD是平行四边形,则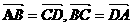
 且
且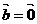 ,则不共线的向量
,则不共线的向量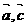 也有
也有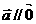 ,
,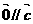 。(8) 不正确, 如图
。(8) 不正确, 如图
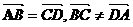 (9)不正确,当
(9)不正确,当