摘要: 如图.在梯形ABCD中.AB//CD.∠BAD=90°.以AD为直径的 半圆O与BC相切. (1)求证:OB丄OC; (2)若AD= 12.∠ BCD=60°.⊙O1与半⊙O 外切.并与BC.CD 相切.求⊙O1的面积. [答案](1)证明:连接OF,在梯形ABCD.在直角△AOB 和直角△AOB F中 ∵ ∴△AOB≌△AOB(HL) 同理△COD≌△COF,∴∠BOC=90°.即OB⊥OC (2) 过点做O1G,O1H垂直DC,DA,∵∠DOB=60°.∴∠DCO=∠BCO=30°.设O1G=x,又∵AD=12,∴OD=6.DC=6,OC=12,CG=x, O1C =6-x,根据勾股定理可知O1G²+GC²=O1C² x²+3x²=(x+6)=0,x=2
网址:http://m.1010jiajiao.com/timu3_id_496064[举报]
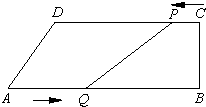 22、已知:如图,在梯形ABCD中,AB∥DC,∠B=90°,BC=8cm,CD=24cm,AB=26Cm,点P从C出发,以1cm/s的速度向D运动,点Q从A出发,以3cm/s的速度向B运 动,其中一动点达到端点时,另一动点随之停止运动.从运动开始.
22、已知:如图,在梯形ABCD中,AB∥DC,∠B=90°,BC=8cm,CD=24cm,AB=26Cm,点P从C出发,以1cm/s的速度向D运动,点Q从A出发,以3cm/s的速度向B运 动,其中一动点达到端点时,另一动点随之停止运动.从运动开始.(1)经过多少时间,四边形AQPD是平行四边形?
(2)经过多少时间,四边形AQPD成为等腰梯形?
(3)在运动过程中,P、Q、B、C四点有可能构成正方形吗?为什么?
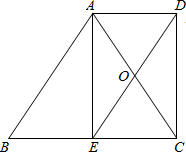 如图,在梯形ABCD中,AD∥BC,BC=2AD,点E是BC的中点,连接AC、DE相交于点O.
如图,在梯形ABCD中,AD∥BC,BC=2AD,点E是BC的中点,连接AC、DE相交于点O.(1)试说明:△AOD≌△COE;
(2)若∠B=
| 1 | 2 |
 9、如图,在梯形ABCD中,DC∥AB,将梯形对折,使点D、C分别落在AB上的点D′、C′,折痕为EF,若CD=3cm,EF=4cm,则AD′+BC′为( )
9、如图,在梯形ABCD中,DC∥AB,将梯形对折,使点D、C分别落在AB上的点D′、C′,折痕为EF,若CD=3cm,EF=4cm,则AD′+BC′为( )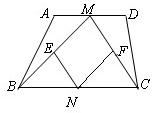 25、如图,在梯形ABCD中,AD∥BC,M,N分别是AD,BC的中点,E,F分别是BM,CM的中点.
25、如图,在梯形ABCD中,AD∥BC,M,N分别是AD,BC的中点,E,F分别是BM,CM的中点. 如图,在梯形ABCD中,AB∥CD,∠A=90°,CD=4,AB=10,
如图,在梯形ABCD中,AB∥CD,∠A=90°,CD=4,AB=10,