2、(2011•南充)学校商店在一段时间内销售了四种饮料共100瓶,各种饮料的销售量如下表:
|
品牌 |
甲 |
乙 |
丙 |
丁 |
|
销售量(瓶) |
12 |
32 |
13 |
43 |
建议学校商店进货数量最多的品牌是( )
A、甲品牌 B、乙品牌
C、丙品牌 D、丁品牌
考点:众数。
专题:常规题型。
分析:根据众数的意义和定义,众数是一组数据中出现次数最多的数据,则进货要进销售量最多的品牌.
解答:解:在四个品牌的销售量中,丁的销售量最多.
故选D.
点评:本题属于基础题,考查了确定一组数据的众数的能力.一些学生往往对这个概念掌握不清楚,而误选其它选项.
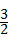 +
+ =﹣2 B、(﹣
=﹣2 B、(﹣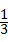 )2=
)2=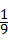
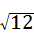 =2
=2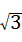
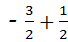 =﹣1,故本答案错误;
=﹣1,故本答案错误;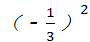 =
=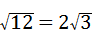 ,故本答案正确.
,故本答案正确.
 ∵y= x2+a
∴x2 = 4a ´ (y– a)=
4ay– 4a2 (6分)
∵y= x2+a
∴x2 = 4a ´ (y– a)=
4ay– 4a2 (6分) 此题为开放题,答案不唯一,只要方案设计合理,可参照给分.
此题为开放题,答案不唯一,只要方案设计合理,可参照给分. 解得:MN =
(7分)
解得:MN =
(7分)