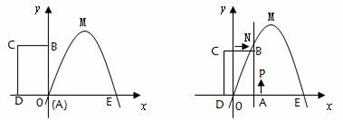
24. 如图1,已知矩形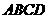 的顶点
的顶点 与点
与点 重合,
重合,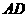 、
、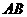 分别在
分别在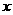 轴、
轴、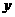 轴上,
轴上,
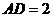 ,
,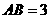 ;抛物线
;抛物线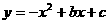 经过坐标原点
经过坐标原点 和
和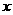 轴上另一点
轴上另一点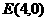
(1)当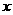 取何值时,该抛物线的最大值是多少?
取何值时,该抛物线的最大值是多少?
(2)将矩形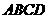 以每秒
以每秒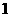
 个单位长度的速度从图
个单位长度的速度从图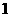 所示的位置沿
所示的位置沿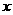 轴的正方向匀速平行移动,同时一动点
轴的正方向匀速平行移动,同时一动点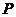 也以相同的速度从点
也以相同的速度从点 出发向
出发向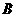 匀速移动.设它们运动的时间为
匀速移动.设它们运动的时间为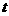 秒(
秒(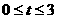 ),直线
),直线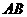 与该抛物线的交点为
与该抛物线的交点为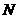 (如图
(如图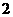 所示).
所示).
|
|
① 当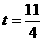 时,判断点
时,判断点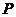 是否在直线
是否在直线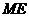 上,并说明理由;
上,并说明理由;
② 以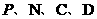 为顶点的多边形面积是否可能为
为顶点的多边形面积是否可能为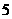 ,若有可能,求出此时
,若有可能,求出此时 点的坐标;若无可能,请说明理由.
点的坐标;若无可能,请说明理由.
21.“知识改变命运,科技繁荣祖国”.我市中小学每年都要举办一届科技运动会.下图为我市某校2010年参加科技运动会航模比赛(包括空模、海模、车模、建模四个类别)的参赛人数统计图:
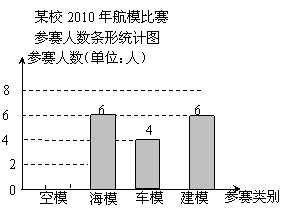

|
(1)该校参加车模、建模比赛的人数分别是 人和 人;
(2)该校参加航模比赛的总人数是 人, 并把条形统计图补充完整;
(3)从全市中小学参加航模比赛选手中随机抽取80人,其中有32人获奖. 今年我市中小学参加航模比赛人数共有2485人,请你估算今年参加航模比赛的获奖人数约是多少人?
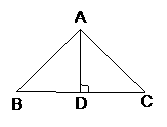
17. 如图, 点是正比例函数
点是正比例函数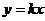 和反比例函数
和反比例函数 的图象的一个交点.
的图象的一个交点.
(1)求这两个函数的解析式;
(2)在反比例函数 的图象上取一点
的图象上取一点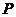 ,过点
,过点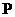 做
做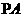 垂直
垂直
于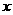 轴,垂足为
轴,垂足为 ,点
,点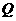 是直线
是直线 上一点,
上一点,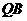 垂直于
垂直于
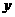 轴,垂足为
轴,垂足为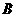 ,直线
,直线 上是否存在这样的点
上是否存在这样的点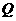 ,使得
,使得
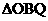 的面积是
的面积是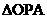 的面积的
的面积的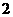 倍?如果存在,请求出
倍?如果存在,请求出
|
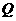 的坐标,如果不存在,请说明理由;
的坐标,如果不存在,请说明理由;
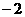 的绝对值是
的绝对值是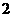 B.
B.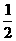 D.
D.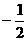
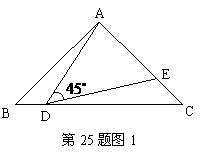 在
在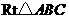 中,
中,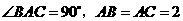 ,点
,点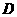 在
在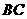 所在的直线上运动,作
所在的直线上运动,作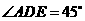 (
(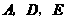 按逆时针方向).
按逆时针方向).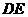 交
交 于
于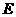 .
.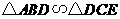 ;
; 是等腰三角形时,求
是等腰三角形时,求 的长.
的长. ,是否存在点
,是否存在点 是等腰三角形?若存在,写出所有点
是等腰三角形?若存在,写出所有点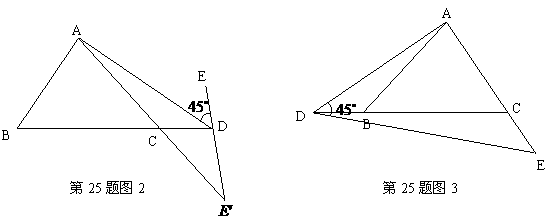 ②如图3,若点
②如图3,若点
 二次方程
二次方程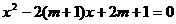
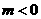 ,且方程的两个实数根分别为
,且方程的两个实数根分别为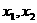 (其中
(其中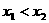 ),若
),若 的函数,且
的函数,且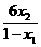 ,求这个函数的解析式;
,求这个函数的解析式;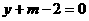 的解.
的解.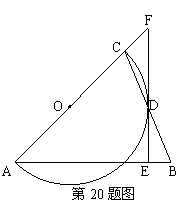 如图,
如图,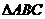 是等腰三角形,
是等腰三角形,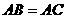 ,以
,以 为
为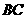 交于点
交于点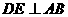 ,垂足为
,垂足为 的延长线与
的延长线与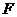 .
.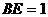 ,求
,求 的值.
的值.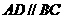 ,
,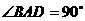 ,
, ,
,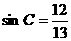 ,
,  000年增加了几倍? (结果精确到整数)
000年增加了几倍? (结果精确到整数)