摘要：如图.点是正比例函数和反比例函数的图象的一个交点. (1)求这两个函数的解析式, (2)在反比例函数的图象上取一点,过点做垂直于轴.垂足为.点是直线上一点.垂直于轴.垂足为.直线上是否存在这样的点.使得的面积是的面积的倍?如果存在.请求出第17题图点的坐标.如果不存在.请说明理由,

网址：http://m.1010jiajiao.com/timu3_id_489451[举报]

如图，已知正比例函数和反比例函数的图象都经过点A（3，3）．
（1）求正比例函数和反比例函数的解析式；
（2）把直线OA向下平移后与反比例函数的图象交于点B（6，m），求m的值和这个一次函数的解析式；
（3）第（2）问中的一次函数的图象与x轴、y轴分别交于C、D，求过A、B、D三点的二次函数的解析式；
（4）在第（3）问的条件下，二次函数在第一象限的图象上是否存在点E，使四边形OECD的面积S₁与四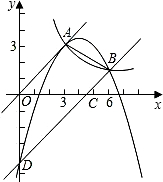

边形OABD的面积S满足：S₁=

S？若存在，求点E的坐标；若不存在，请说明理由．查看习题详情和答案>>

如图，已知正比例函数和反比例函数的图象都经过点M（-3，-1），且知点P（-1，-

3）是反比例函数图象上的点：
（1）分别求出正比例函数和反比例函数的解析式；
（2）作PA⊥x轴，垂足为A，当点Q在直线MO上运动时，作QB⊥y轴，垂足为B，问：直线MO上是否存在这样的点Q，使得△OBQ与△OAP面积相等？如果存在，请求出点Q的坐标，如果不存在，请说明理由；
（3）当点Q在第一象限中的双曲线上运动时，作以OP、OQ为邻边的?OPCQ，求?OPCQ周长的最小值以及取得最小值时点Q的坐标．查看习题详情和答案>>

如图，已知正比例函数和反比例函数的图象都经过点M（-2，-1），且P（-1，-2）为双曲线上的一点

，Q为坐标平面上一动点，PA垂直于x轴，QB垂直于y轴，垂足分别是A、B．
（1）写出正比例函数和反比例函数的关系式；
（2）当点Q在直线MO上运动时，直线MO上是否存在这样的点Q，使得△OBQ与△OAP面积相等？如果存在，请求出点的坐标；如果不存在，请说明理由．查看习题详情和答案>>

如图，已知正比例函数和反比例函数的图象都经过点M（-2，-1），且点P（-1，-2）为双曲线上的一点，过P作PA垂直x轴于点A：
（1）写出正比例函数和反比例函数的关系式；
（2）若点Q为直线MO上一动点（不与点M、O重合），过点Q作QB⊥y轴于点B，是否存在点Q，使△OBQ与△OAP面积相等？如果存在，请求出点Q的坐标；如果不存在，请说明理由；
（3）在（2）的条件下，在平面内找一点C，使以O、P、C、Q为顶点的四边形为平行四边形，请直接写出C点坐标．

查看习题详情和答案>>

如图，已知正比例函数和反比例函数的图象都经过点M（-3，-1），且知点P（-1，-3）是反比例函数图象上的点：
（1）分别求出正比例函数和反比例函数的解析式；
（2）作PA⊥x轴，垂足为A，当点Q在直线MO上运动时，作QB⊥y轴，垂足为B，问：直线MO上是否存在这样的点Q，使得△OBQ与△OAP面积相等？如果存在，请求出点Q的坐标，如果不存在，请说明理由；
（3）当点Q在第一象限中的双曲线上运动时，作以OP、OQ为邻边的?OPCQ，求?OPCQ周长的最小值以及取得最小值时点Q的坐标．

查看习题详情和答案>>